山东省济宁市泗水县2021-2022学年七年级上学期期中数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
1. “你以为你已经很爱很爱妈妈了,但妈妈远比你想象中更爱更爱更爱你”.这是2021年2月12日大年初一全国上映的电影《你好,李焕英》中的一句话,这部电影首日票房就达298000000元,数字298000000用科学记数法可表示为( )A、 B、 C、 D、2. 下列各式中,运算正确的是( )A、 B、 C、 D、3. 点 在数轴上表示的数为-3,若一个点从点 移动4个单位长度,此时终点所表示的数是( )A、-7或-1 B、1 C、7 D、1或-74. 下列各组数中,相等的是( )A、-1与(-4)+(-3) B、 与-(-3) C、 与 D、 与-165. 如果|x﹣2|+(y+ )2=0,那么yx的值为( )A、 B、﹣ C、 D、﹣6. 用四舍五入法按要求对0.3056分别取近似值,其中正确的是( )A、0.30(精确到0.01) B、0.31(精确到百分位) C、0.305(精确到0.001) D、0.31(精确到0.001)7. 下列说法中,正确的是( )A、单项式 xy2的系数是 B、单项式﹣6x2的次数为﹣6 C、多项式x3+2x+18是三次三项式 D、多项式3x2+y2﹣2的常数项是28. 如果 与 是同类项,那么 的值是( )A、3 B、2 C、0 D、-19. 若 ,则 的值是( )A、3 B、2 C、1 D、-110. 有理数 在数轴上的位置如图所示,下列各数中,① ;② ;③ ;④ ,在0到1之间数的个数是( )
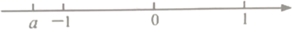 A、1 B、2 C、3 D、411. 我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,例如将 , 换算成十进制数应为:
A、1 B、2 C、3 D、411. 我们常用的数是十进制数,计算机程序使用的是二进制数(只有数码0和1),它们两者之间可以互相换算,例如将 , 换算成十进制数应为:;
.
按此方式,将二进制 换算成十进制数的结果为( )
A、17 B、9 C、10 D、1812. 如图所示的运算程序中,若开始输入 的值为 ,则第 次输出的结果为( )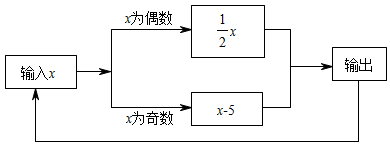 A、-6 B、-3 C、-8 D、-2
A、-6 B、-3 C、-8 D、-2二、填空题
-
13. 《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,若收入60元记作+60元,则支出20元应该表示为 .14. 已知 、 互为相反数, 、 互为倒数,那么 .15. 一个多项式 与 的和是 ,则这个多项式 为 .16. 如果关于字母 的多项式 的值与 的值无关,则 .17. 有理数 , , 在数轴上的位置如图所示,化简 的值为 .
 18. 如图,是由形状相同的正六边形和正三角形组成的一组有规律的图案,则第 个图案中正六边形和正三角形的个数和是 .
18. 如图,是由形状相同的正六边形和正三角形组成的一组有规律的图案,则第 个图案中正六边形和正三角形的个数和是 .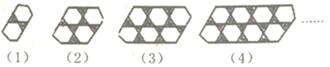
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 化简:(1)、 ;(2)、 .21. 先化简,再求值: ,其中 , .22. 某同学在计算一个多项式减去 时,误认为加上此式,计算出的错误结果为 ,试求出这个多项式,并求出正确结果.23. 定义一种新运算:1☆3=1×2+3=5,3☆(-1)=3×2-1=5,5☆4=5×2+4=14,4☆(-2)=4×2-2=6.(1)、观察上面各式,用字母表示上面的规律:a☆b=;(2)、若a≠b,则a☆bb☆a(填“=”或“≠”);(3)、若(3a)☆(-2b)=-6,则3a-b= , 并求(3a-2b)☆(3a+b)的值.24. 开学伊始,学校决定对上学期期末考试成绩优秀的学生和进步大的学生进行表彰,总务处李老师计划购买一些笔记本作为奖品,他去两家文体商店对笔记本的价格进行了咨询:
商店A:购买本数不超过100本时,每本5元;超过100本时,超过的部分每本4元.
商店B:无论买多少本,每本4.5元.
(1)、设购买的笔记本为x本,用含有x的代数式分别表示两家商店所需要的费用.(2)、若学校要购买300本笔记本,应该去哪家商店比较合算?说明理由.25. 下表记录的是黑河今年某一周内的水位变化情况,上周末(上个星期日)的水位已达到15米,(正号表示水位比前一天上升,负号表示水位比前一天下降)星期
一
二
三
四
五
六
日
水位变化(米)
+0.2
+0.8
﹣0.4
+0.2
+0.3
﹣0.5
﹣0.2
(1)、本周最高水位是米,最低水位是米;(2)、与上周末相比,本周末河流的水位是 . (填“上升了”或“下降了”)(3)、由于下周将有大降雨天气,工作人员预测水位将会以每小时0.05米的速度上升,当水位达到16.8米时,就要开闸泄洪,请你计算一下,再经过多少个小时工作人员就需要开闸泄洪?26. 定义:若 , , 为数轴上三点,若点 到点 的距离是点 到点 的距离2倍,我们就称点 是 的美好点.例如;如图1,点 表示的数为-1,点 表示的数为2.表示1的点 到点 的距离是2,到点 的距离是1,那么点 是 的美好点;又如,表示0的点 到点 的距离是1,到点 的距离是2,那么点 就不是 的美好点,但点 是 的美好点.
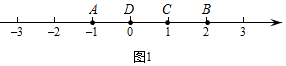
如图2, , 为数轴上两点,点 所表示的数为 ,点 所表示的数为 .
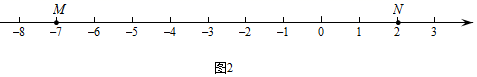
 (1)、点 , , 表示的数分别是 , , ,其中是 美好点的是;写出 美好点 所表示的数是 .(2)、现有一只电子蚂蚁 从点 开始出发,以 个单位每秒的速度向左运动.当 为何值时,点 恰好为 的美好点?
(1)、点 , , 表示的数分别是 , , ,其中是 美好点的是;写出 美好点 所表示的数是 .(2)、现有一只电子蚂蚁 从点 开始出发,以 个单位每秒的速度向左运动.当 为何值时,点 恰好为 的美好点?