山东省东营市广饶县(五四制)2021-2022学年七年级上学期期中考试数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三条线段,不能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,3. 下列各组数中,以它们为边长的线段能构成直角三角形的是( )A、12、15、18 B、6、8、12 C、4、5、6 D、7、24、254. 如图,在△ABC中,画出AC边上的高,正确的图形是( )A、
2. 下列长度的三条线段,不能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,3. 下列各组数中,以它们为边长的线段能构成直角三角形的是( )A、12、15、18 B、6、8、12 C、4、5、6 D、7、24、254. 如图,在△ABC中,画出AC边上的高,正确的图形是( )A、 B、
B、 C、
C、 D、
D、 5. 点D、E分别在级段AB、AC上,CD与BE相交于点O,已知AB=AC,添加以下哪一个条件不能判定△ABE≌△ACD( )
5. 点D、E分别在级段AB、AC上,CD与BE相交于点O,已知AB=AC,添加以下哪一个条件不能判定△ABE≌△ACD( ) A、∠B=∠C B、∠BEA=∠CDA C、BE=CD D、CE=BD6. 已知∠AOB,用尺规作一个角∠A’O’B’等于已知角∠AOB的作图痕迹如图所示,则判断∠AOB=∠A’O’B’所用到的三角形全等的判断方法是( )
A、∠B=∠C B、∠BEA=∠CDA C、BE=CD D、CE=BD6. 已知∠AOB,用尺规作一个角∠A’O’B’等于已知角∠AOB的作图痕迹如图所示,则判断∠AOB=∠A’O’B’所用到的三角形全等的判断方法是( ) A、SAS B、ASA C、AAS D、SSS7. 如图,直线是一条河,A、B是两个新农村定居点.欲在l上的某点处修建一个水泵站,由水泵站直接向A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是( )
A、SAS B、ASA C、AAS D、SSS7. 如图,直线是一条河,A、B是两个新农村定居点.欲在l上的某点处修建一个水泵站,由水泵站直接向A、B两地供水.现有如下四种管道铺设方案,图中实线表示铺设的供水管道,则铺设管道最短的方案是( ) A、
A、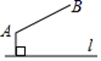 B、
B、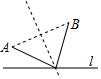 C、
C、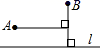 D、
D、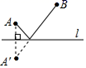 8. 已知∠AOB= 60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点M,N为圆心,以大于 MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )A、15° B、45° C、15°或30° D、15°或45°9. 如图,一圆柱高 ,底面半径为 ,一只蚂蚁从点 爬到点 处吃食,要爬行的最短路程( 取3)是( )
8. 已知∠AOB= 60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点M,N为圆心,以大于 MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )A、15° B、45° C、15°或30° D、15°或45°9. 如图,一圆柱高 ,底面半径为 ,一只蚂蚁从点 爬到点 处吃食,要爬行的最短路程( 取3)是( ) A、 B、 C、 D、无法确定10. 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),以下五个结论正确的个数是( )
A、 B、 C、 D、无法确定10. 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),以下五个结论正确的个数是( )①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤ .
 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 已知等腰三角形的两边长分别是2和6,则它的周长是 .12. 如图,在 中,AB的垂直平分线DE交AB于点D , 交AC于点E , 且 , 的周长等于 ,则 的长度等于 .
 13. 如图,AD是△ABC的中线,CE是△ACD的中线,S△ACE=3cm2 , 则S△ABC=cm2 .
13. 如图,AD是△ABC的中线,CE是△ACD的中线,S△ACE=3cm2 , 则S△ABC=cm2 . 14. 如图, 是 的两条角平分线, ,则 的度数为 .
14. 如图, 是 的两条角平分线, ,则 的度数为 . 15. 正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有种.
15. 正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有种. 16. 如图所示,在高为3m,斜坡长为5m的楼梯表面铺地毯,至少需要地毯米.
16. 如图所示,在高为3m,斜坡长为5m的楼梯表面铺地毯,至少需要地毯米. 17. 如图,∠AOB=30°,P是∠AOB的角平分线上的一点,PM⊥OB于点M,PN∥OB交OA于点N,若PM=1,则PN= .
17. 如图,∠AOB=30°,P是∠AOB的角平分线上的一点,PM⊥OB于点M,PN∥OB交OA于点N,若PM=1,则PN= . 18. 如图,已知 ,点 、 、 …在射线ON上,点 、 、 …在射线 上, 、 、 …均为等边三角形,若 ,则 的边长为 .
18. 如图,已知 ,点 、 、 …在射线ON上,点 、 、 …在射线 上, 、 、 …均为等边三角形,若 ,则 的边长为 .
三、解答题
-
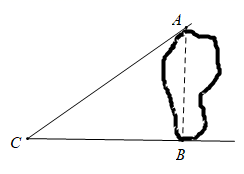
19. 如图,湖的两岸有A , B两点,在与AB成直角的BC方向上的点C处测得 米, 米.求A , B两点间的距离.
 20. 尺规作图:
20. 尺规作图:已知:如图, ,线段b , 线段c .
求作: ,使得 , , .
要求:不要求写出作法,保留作图痕迹.
 21. 如图,已知 中, , , 边上的垂直平分线 交 于点 ,交 于 .
21. 如图,已知 中, , , 边上的垂直平分线 交 于点 ,交 于 .
求:
(1)、 的度数;(2)、若 ,求 的长.22. 我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m. (1)、求出空地ABCD的面积.(2)、若每种植1平方米草皮需要200元,问总共需投入多少元?23. 如图,已知 为等边三角形(三条边相等三个角为 的三角形),点D、E分别在BC、AC边上,且 ,AD与BE相交于点F .
(1)、求出空地ABCD的面积.(2)、若每种植1平方米草皮需要200元,问总共需投入多少元?23. 如图,已知 为等边三角形(三条边相等三个角为 的三角形),点D、E分别在BC、AC边上,且 ,AD与BE相交于点F . (1)、求证: ;(2)、求 的度数.24. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)、求证: ;(2)、求 的度数.24. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上. (1)、在图中画出与 关于直线l成轴对称的 ,并在所画图中标明字母;(2)、 的面积为;(3)、在直线l上找一点P , 连接PB、PC , 当 最小时,这个最小值是.25. 已知△ABC和△ADE都是等腰直角三角形,点D是直线BC上的一动点(点D不与B、C重合),连接CE,
(1)、在图中画出与 关于直线l成轴对称的 ,并在所画图中标明字母;(2)、 的面积为;(3)、在直线l上找一点P , 连接PB、PC , 当 最小时,这个最小值是.25. 已知△ABC和△ADE都是等腰直角三角形,点D是直线BC上的一动点(点D不与B、C重合),连接CE,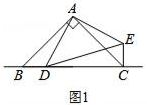
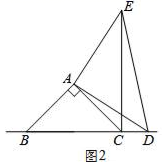
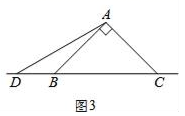 (1)、在图1中,当点D在边BC上时,求证:BC=CE+CD;(2)、在图2中,当点D在边BC的延长线上时,结论BC=CE+CD是否还成立?若不成立,请猜想BC、CE、CD之间存在的数量关系,并说明理由;(3)、在图3中,当点D在边BC的反向延长线上时,补全图形,不需写证明过程,直接写出BC、CE、CD之间存在的数量关系.26. 已知CD是经过∠BCA顶点C的一条直线,CA=CB . E、F分别是直线CD上两点,且∠BEC=∠CFA=∠ .
(1)、在图1中,当点D在边BC上时,求证:BC=CE+CD;(2)、在图2中,当点D在边BC的延长线上时,结论BC=CE+CD是否还成立?若不成立,请猜想BC、CE、CD之间存在的数量关系,并说明理由;(3)、在图3中,当点D在边BC的反向延长线上时,补全图形,不需写证明过程,直接写出BC、CE、CD之间存在的数量关系.26. 已知CD是经过∠BCA顶点C的一条直线,CA=CB . E、F分别是直线CD上两点,且∠BEC=∠CFA=∠ . (1)、若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
(1)、若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:①如图1若∠BCA=90°,∠ =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
②如图2,若0°<∠BCA<180°, 请添加一个关于∠ 与∠BCA关系的条件,使①中的结论仍然成立;
(2)、如图3,若直线CD经过∠BCA的外部,∠ =∠BCA , 请写出三条线段EF、BE、AF的数量关系并证明你的结论.