辽宁省沈阳市于洪区2021-2022学年七年级上学期期中数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
1. 下面给出的图形中,绕虚线旋转一周能形成圆锥的是( )A、
 B、
B、 C、
C、 D、
D、 2. 的相反数是( )A、-5 B、5 C、 D、-3. 已知代数式﹣3xm﹣1y3与4xym+n是同类项,那么m , n的值分别为( )A、m=2,n=﹣1 B、m=2,n=1 C、m=﹣2,n=﹣1 D、m=﹣2,n=14. 下列图形经过折叠不能围成棱柱的是( )A、
2. 的相反数是( )A、-5 B、5 C、 D、-3. 已知代数式﹣3xm﹣1y3与4xym+n是同类项,那么m , n的值分别为( )A、m=2,n=﹣1 B、m=2,n=1 C、m=﹣2,n=﹣1 D、m=﹣2,n=14. 下列图形经过折叠不能围成棱柱的是( )A、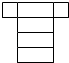 B、
B、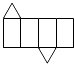 C、
C、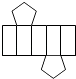 D、
D、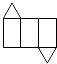 5. 多项式 中次数最高的项的系数( )A、5 B、4 C、3 D、-46. 下列计算正确的是( )A、﹣5+6=11 B、﹣8﹣8=0 C、 D、0÷(﹣2)=07. 已知a2+5a=1,则代数式3a2+15a﹣1的值为( )A、0 B、1 C、2 D、38. 下列说法正确的是( )A、有理数分为正数和负数 B、互为相反数的两个数的绝对值相等 C、两数相加,和一定大于任何一个加数 D、两数相减,差一定小于被减数9. 实数a,b在数轴上的位置如图所示,下列结论中正确的是( )
5. 多项式 中次数最高的项的系数( )A、5 B、4 C、3 D、-46. 下列计算正确的是( )A、﹣5+6=11 B、﹣8﹣8=0 C、 D、0÷(﹣2)=07. 已知a2+5a=1,则代数式3a2+15a﹣1的值为( )A、0 B、1 C、2 D、38. 下列说法正确的是( )A、有理数分为正数和负数 B、互为相反数的两个数的绝对值相等 C、两数相加,和一定大于任何一个加数 D、两数相减,差一定小于被减数9. 实数a,b在数轴上的位置如图所示,下列结论中正确的是( )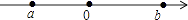 A、a>b B、|a|>|b| C、﹣a<b D、a+b<010. 某件商品的成本价为a元,按成本价提高15%后标价,又以8折销售,这件商品的售价( )A、比成本价低了0.08a元 B、比成本价低了0.2a元 C、比成本价高了0.15a元 D、与成本价相同
A、a>b B、|a|>|b| C、﹣a<b D、a+b<010. 某件商品的成本价为a元,按成本价提高15%后标价,又以8折销售,这件商品的售价( )A、比成本价低了0.08a元 B、比成本价低了0.2a元 C、比成本价高了0.15a元 D、与成本价相同二、填空题
-
11. 如图是一个正方体的表面沿着某些棱剪开后展成的一个平面图形,若这个正方体的每两个相对面上的数字的和都是8,则y= .
 12. 科学防疫从勤洗手开始,一双没洗干净的手上带有各种细菌病毒大约850000000个,将数据850000000用科学记数法表示为 .13. 长方形的长为 ,宽比长少 ,则这个长方形的周长是 .14. 某路公交车从起点经过A , B , C , D站到达终点,各站上下乘客的人数如下(上车为正,下车为负):起点(20,0),A(12,﹣4),B(8,﹣9),C(6,﹣4),D(2,﹣7),终点(0,).15. 一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,则该几何体至少是用 个小立方块搭成的.
12. 科学防疫从勤洗手开始,一双没洗干净的手上带有各种细菌病毒大约850000000个,将数据850000000用科学记数法表示为 .13. 长方形的长为 ,宽比长少 ,则这个长方形的周长是 .14. 某路公交车从起点经过A , B , C , D站到达终点,各站上下乘客的人数如下(上车为正,下车为负):起点(20,0),A(12,﹣4),B(8,﹣9),C(6,﹣4),D(2,﹣7),终点(0,).15. 一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,则该几何体至少是用 个小立方块搭成的.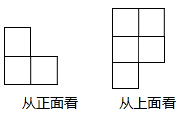 16. 有一种“二十四点”游戏,其游戏规则是:任取1至13之间的四个自然数,将这四个数(每个数用且只用一次,可以加括号)进行混合运算,使其结果等于24或﹣24.现有四个数﹣6,3,4,10,可通过算式:使其结果等于24.
16. 有一种“二十四点”游戏,其游戏规则是:任取1至13之间的四个自然数,将这四个数(每个数用且只用一次,可以加括号)进行混合运算,使其结果等于24或﹣24.现有四个数﹣6,3,4,10,可通过算式:使其结果等于24.三、解答题
-
17. 计算:(1)、42﹣(﹣38)+(﹣27)﹣65;(2)、14÷( )﹣3×(﹣8);(3)、( )÷( );(4)、﹣14 ( )÷(﹣3)2 .18. 化简:(1)、a2+(3a﹣5)﹣(4a﹣1);(2)、﹣2(a2b ab2 a3)﹣(﹣2a2b+3ab2).19. 已知A=xy﹣2y2+3x2 , B=xy﹣4y2 , C=2B﹣5A .(1)、求C的表达式;(2)、当x=﹣1,y ,求C的值.20. 某零件厂现生产A , B两种尺寸的零件,两种零件的成本和售价如表:
成本(元/个)
售价(元/个)
A
50
80
B
70
90
该厂每天共生产A , B两种尺寸的零件800个,设每天生产A种零件x个.
(1)、用含x的代数式表示该厂每天的生产成本,并进行化简;(2)、用含x的代数式表示该厂每天获得的利润,并进行化简;(3)、当x=500时,求该厂每天获得的利润.(利润=售价﹣成本)21. 定义一种新运算:a⊗m=a×|m|.如5⊗(﹣3)=5×|﹣3|=15,﹣8⊗4=﹣8×|4|=﹣32.
(1)、计算:65⊗0= , ﹣43⊗|﹣2|=;(2)、若n<0,化简48⊗(﹣3n);(3)、若a , m , n为任意有理数,等式a⊗(m+n)=a⊗m+a⊗n一定成立吗?请说理由.22. 如图,相距10km的A , B两地间有一条笔直的公路,C地位于A , B两地间且距A地6km,小明骑单车从A地出发沿公路以每小时5km的速度向B地匀速骑行,当到达B地后立即以原来的速度返回,直到A地停止.设小明骑行时间为t(h),小明所处位置记为点P . 若以C地为原点,以从A到B为正方向,用1个单位长度表示1km,在数轴上表示A , B , C三地,解答下列问题: (1)、填空:点A表示的有理数为 , 点B表示的有理数为 ;(2)、当t=0.5时,点P表示的有理数为 ;(3)、在小明由A地到B地过程中,点P表示的有理数为 , 在小明由B地返回A地过程中,点P表示的有理数为 (用含的代数式表示);(4)、当小明距离C地2km时,请直接写出所有满足条件的值.
(1)、填空:点A表示的有理数为 , 点B表示的有理数为 ;(2)、当t=0.5时,点P表示的有理数为 ;(3)、在小明由A地到B地过程中,点P表示的有理数为 , 在小明由B地返回A地过程中,点P表示的有理数为 (用含的代数式表示);(4)、当小明距离C地2km时,请直接写出所有满足条件的值.