天津市红桥区第二学区2021-2022学年八年级上学期期中考试数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下各组长度的线段为边,能构成三角形的是( )A、8cm、5cm、3cm B、6cm、8cm、15cm C、8cm、4cm、3cm D、4cm、6cm、5cm3. 若一个多边形的内角和等于 ,这个多边形的边数是( )A、6 B、8 C、10 D、124. 如图,AB∥DE,∠BCE=53°,∠E=25°,则∠B的度数为( )
2. 以下各组长度的线段为边,能构成三角形的是( )A、8cm、5cm、3cm B、6cm、8cm、15cm C、8cm、4cm、3cm D、4cm、6cm、5cm3. 若一个多边形的内角和等于 ,这个多边形的边数是( )A、6 B、8 C、10 D、124. 如图,AB∥DE,∠BCE=53°,∠E=25°,则∠B的度数为( ) A、25° B、28° C、30° D、33°5. 如图,若 ≌ , , ,则CE的长为( )
A、25° B、28° C、30° D、33°5. 如图,若 ≌ , , ,则CE的长为( ) A、1.5 B、2 C、2.5 D、3.56. 如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定 的是( )
A、1.5 B、2 C、2.5 D、3.56. 如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定 的是( ) A、AM=CN B、 C、AB=CD D、∠M=∠N7. 如图, ,点 和点 ,点 和点 是对应点. ,则 的度数为( )
A、AM=CN B、 C、AB=CD D、∠M=∠N7. 如图, ,点 和点 ,点 和点 是对应点. ,则 的度数为( ) A、20° B、30° C、35° D、40°8. 如图,6个边长相等正方形的组合图形,则 的度数( )
A、20° B、30° C、35° D、40°8. 如图,6个边长相等正方形的组合图形,则 的度数( )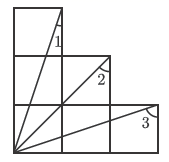 A、45° B、90° C、135° D、225°9. 如图所示,在△ABC中,∠C=90°,AD平分∠BAC , DE⊥AB于E , DE=4,BC=9,则BD的长为( )
A、45° B、90° C、135° D、225°9. 如图所示,在△ABC中,∠C=90°,AD平分∠BAC , DE⊥AB于E , DE=4,BC=9,则BD的长为( ) A、6 B、5 C、4 D、310. 如图,在 中, 、 的垂直平分线分别交 于点 、 ,若 ,则 为( )
A、6 B、5 C、4 D、310. 如图,在 中, 、 的垂直平分线分别交 于点 、 ,若 ,则 为( ) A、38° B、40° C、24° D、44°11. 如图,在等边三角形 中, , 分别是 , 的中点,点 是线段 上的一个动点,当 的周长最小时, 点的位置在( )
A、38° B、40° C、24° D、44°11. 如图,在等边三角形 中, , 分别是 , 的中点,点 是线段 上的一个动点,当 的周长最小时, 点的位置在( ) A、 点处 B、 点处 C、 的中点处 D、 三条高的交点处12. 如图,已知 , , , , 和 交于 点,则下列结论:① ;② ;③ 平分 ;④ .其中正确的有( )
A、 点处 B、 点处 C、 的中点处 D、 三条高的交点处12. 如图,已知 , , , , 和 交于 点,则下列结论:① ;② ;③ 平分 ;④ .其中正确的有( ) A、①② B、①②③ C、①②③④ D、①②④
A、①② B、①②③ C、①②③④ D、①②④二、填空题
-
13. 已知点P(3,﹣1)关于y轴的对称点Q的坐标是.14. 若一个多边形的内角和等于它的外角和,则这个多边形的边数为.15. 如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=10,CF=2,则AC= .
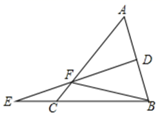 16. 已知等腰三角形中,一腰上的中线将三角形的周长分成6cm和9cm两部分,则这个三角形的腰长为 cm.17. 如图,在等边三角形ABC中,BD=CE,AD,BE交于点F,则 ;
16. 已知等腰三角形中,一腰上的中线将三角形的周长分成6cm和9cm两部分,则这个三角形的腰长为 cm.17. 如图,在等边三角形ABC中,BD=CE,AD,BE交于点F,则 ;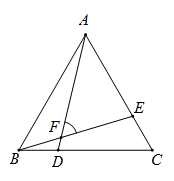 18. 如图, 是 的角平分线, 垂足为 , , 和 的面积分别为68和42,则 的面积为 .
18. 如图, 是 的角平分线, 垂足为 , , 和 的面积分别为68和42,则 的面积为 .
三、解答题
-
19. 如图,在平面直角坐标系中, , , .
 (1)、 的面积;(2)、在坐标系中作出 关于 轴对称的 ,并写出点 、 、 的坐标.20. 如图,AB=AE,∠B=∠AED,∠1=∠2.求证:△ABC≌△AED.
(1)、 的面积;(2)、在坐标系中作出 关于 轴对称的 ,并写出点 、 、 的坐标.20. 如图,AB=AE,∠B=∠AED,∠1=∠2.求证:△ABC≌△AED.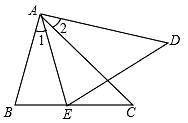 21. 如图,在 和 中, , 为 上一点, , .求证: .
21. 如图,在 和 中, , 为 上一点, , .求证: . 22. 嘉琪在学习过程中,对教材的一个有趣的问题做如下探究:
22. 嘉琪在学习过程中,对教材的一个有趣的问题做如下探究:(习题回顾)
已知:如图,在 中, ,角平分线 、 交于点 .求 的度数.
 (1)、请直接写出 ;(2)、(变式思考)若 ,请猜想 与 的关系,并说明理由.
(1)、请直接写出 ;(2)、(变式思考)若 ,请猜想 与 的关系,并说明理由.

