山西省吕梁市孝义市2021-2022学年八年级上学期期中数学试题
试卷更新日期：2021-11-24 类型：期中考试
一、单选题
-
1. 下列交通标志中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 以下四组图形中，与如下图形全等的是（ ）
A、
B、
C、
D、
3. 小明要做一个三角形木架，现在他已经有长度为20cm和40cm的两根木条，那么下列可供他选用的木条的长是（ ）A、20cm B、40cm C、60cm D、80cm4. 八边形的外角和是（ ）A、180° B、360° C、540° D、720°5. 一个等边三角形和两个等腰直角三角形的位置如图所示，若∠3＝70°，则∠1＋∠2＝（ ）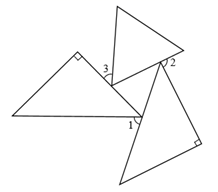
A、290° B、200° C、140° D、110°6. 如图，∠C＝∠D＝90°，AC＝BD，则判定 ABC≌ BAD全等的依据是（ ）
A、SAS B、ASA C、AAS D、HL7. 已知点A(m，2)和点B(－1，n)关于y轴对称，则m＋n的值是（ ）A、1 B、－3 C、3 D、－18. 如图，在 ABC中，AB＝8，BC＝9，AC＝6，AD是角平分线，DE⊥AB，DF⊥AC，则 （ ）
A、4：3 B、9：8 C、9：6 D、3：29. 如图， ABC中，点E是AC的中点、点F是中线CD的中点，若 DEF的面积是3，则 ABC的面积是（ ）
A、12 B、24 C、36 D、4810. 如图，在 ABC中，DE是AB的垂直平分线，BC上的点F在AC的垂直平分线上，若AB＝6，AC＝8，BC＝12，则 AEF的周长是（ ）
A、6 B、8 C、10 D、12二、填空题
-
11. 如图，点D，E分别在线段AB，AC上，且AB＝AC，要依据“AAS”判定 ABE≌ ACD，则还需要添加的条件是 ．
12. 如图，停放自行车时要放下支架，自行车之所以能停放稳定，是因为构成了三个三角形：一是由前轮与地面的接触点、后轮与地面的接触点、支架与地面的接触点构成的三角形支撑面；二是自行车车架呈三角形；三是由后轮、轴、支架所构成的三角形．其中，蕴含的数学道理是 ．
13. 如图，过正五边形ABCDE的顶点A作直线l∥BE，则∠1的度数为 ．
14. 如图，直角坐标系中，已知A(－2，－1)，B(3，－1)，C(1，2)，请你在y轴上找一点P．使 ABP和 ABC全等，则点P的坐标是 ． （写出一个即可）
15. 如图，一个等腰直角三角形ABC物件斜靠在墙角处（∠O＝90°），若OA＝50cm，OB＝28cm，则点C离地面的距离是 cm．
16. 如图，以△ABC的顶点A为圆心，适当长为半径画弧，分别交AB，AC于点D，E，再分别以D，E为圆心，大于 DE的长为半径画弧，两弧交于点F，作射线AF交BC于点G，若AB＝AG＝GC，则∠AGC＝ ．
三、解答题
-
17. 如图，CE是 ABC的外角∠ACD的平分线，且CE交BA的延长线于点E，AF是△ABC的高，∠B＝30°，∠E＝40°，求∠ECD和∠FAC的度数．
18. 如图，∠ABC＝∠DCB，BD、CA分别平分∠ABC、∠DCB．求证：AC＝DB．
19. 作图题：如图，已知 ABC，在BC上找一点D，使 ABD的周长等于AB＋BC．（尺规作图，不写作法，保留作图痕迹）
20. 如图， ABC中，已知点A(－2，0)，B(3，2)，C(2，4)．
⑴作出 ABC关于x轴对称的 ，并写出点 的坐标；
⑵作出 ABC关于直线x＝1对称的 ，并写出点 的坐标；
⑶观察猜想： 和 的数量关系和位置关系： ▲ ． （直接写出答案）
21. 下面是小明解决一道课本练习题的过程及反思，请认真阅读并完成相应学习任务．一道课后练习题的解答与思考：如图，要测量池塘两岸相対两点A，B的距离，可以在池塘外取AB的垂线BF上的两点C，D，使BC＝CD，再画出BF的垂线DE，使E与A，C在一条直线上，这时测得DE的长就是AB的长．为什么？
理由如下：∵AB⊥BD，ED⊥BD，
∴∠ABC＝∠EDC＝90°．
∴在 ABC和 EDC中，
∴ ABC≌ EDC（依据1）
∵AB＝ED（依据2）
∴测得DE的长就是AB的长．
反思：由于本题中AB ED，且C为BD的中点，因而可以用全等三角形的有关知识把AB的长度转化为DE的长度．所以当我们遇到“平行线和中点”的有关问题时，常常可以构造“X”型全等三角形解决问题，达到转化线段或角的目的．
(1)、任务一：上述材料中的依据1，依据2分别指的是什么？①依据1：；
②依据2： ．
(2)、任务二：如图，四边形ABCD中，AD BC，点E是CD的中点，AE⊥BE．求证：AB＝AD＋BC．
22. 综合与实践：如图1， ABC中，∠C＝90°，AC＝BC．点D是AB的中点，点E是CB上一点（不与点B，C重合），连接DE，以DE为直角边作等腰直角三角形DEF，其中∠EDF＝90°，DE＝DF．连接BF．(1)、求证：BF＝CE，BF⊥CE．
(2)、如图2，若点E在CB的延长线上，其他条件不变，BF与CE有怎样的数量关系和位置关系？请说明理由；
(3)、如图3在（2）的基础上，当FB平分∠DFE时，若BE＝3，则EC＝ ． （直接写出答案）