山西省吕梁市交城县2021-2022学年八年级上学期期中考试数学试题

试卷更新日期：2021-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. 已知三角形三边的长都是整数，且周长是12，则三边的长不可能是（）

A、2，5，5 B、3，3，6 C、3，4，5 D、4，4，4

查看试题解析
2. 一个多边形从一个顶点引出的对角线条数是4，这个多边形的边数是（）

A、4 B、5 C、6 D、7

查看试题解析
3. 自新冠肺炎疫情发生以来，全国人民共同抗疫，各地积极普及科学防控知识．下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，△ABC和△DEF中，AB＝DE，∠B＝∠E，下列哪一个条件无法证明△ABC≌△DEF（）

A、BF＝CE B、∠A＝∠D C、∠ACB＝∠DFE D、AC＝DF

查看试题解析
5. 如图，某小区有甲、乙两座楼房，在乙楼底部B点测得甲楼顶部D点的仰角为64°，且发现DB正好是∠CDA的角平分线，求站在乙楼顶A点处时测得甲楼顶部D点的仰角为（）

A、52° B、26° C、38° D、32°

查看试题解析
6. 如图，直线 $M N$ 是四边形 $A M B N$ 的对称轴，点 $P$ 是直线 $M N$ 上的点，下列判断错误的是（）

A、 $A M = B M$ B、 $∠ M A P = ∠ M B P$ C、 $∠ A N M = ∠ B N M$ D、 $A P = B N$

查看试题解析
7. 探究多边形的内角和时，需要把多边形分割成若干个三角形．在分割六边形时，所分三角形的个数不可能的是（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
8. 点A（－2021，1）关于 $y$ 轴对称的点的坐标是（）

A、（－2021，1） B、（2021，－1） C、（2021，1） D、（－2021，－1）

查看试题解析
9. 如图，在正方形网格中有M，N两点，在直线 $l$ 上求一点P使PM＋PN最短，则点P应选在（）

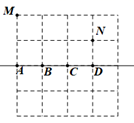A、A点 B、B点 C、C点 D、D点

查看试题解析
10. 把△ABC和△ADE如图放置，B，D，E正好在一条直线上，AB＝AC，AD＝AE，∠BAC＝∠DAE．则下列结论：①△BAD≌△CAE；②BE＝CE＋DE；③∠BEC＝∠BAC；④若∠ACE＋∠CAE＋∠ADE＝90°，则∠AEC＝135°．其中正确的是（）

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析

二、填空题

11. 木工师傅做了一个高凳，用于攀高工作，小明看到了建议再加几根木条（如图所示），说这样更安全．你知道小明这样建议的原理是．

查看试题解析
12. 已知一个包装盒的底面是内角和为720°的多边形，它是由另一个多边形纸片剪掉一个角以后得到的，则原多边形是边形．

查看试题解析
13. 如图所示，在△ABC中，AB＝AC，∠B＝50°，则∠A＝．

查看试题解析
14. 在△ABC中，∠A＝∠B，∠A＋∠C＝3∠B，则△ABC的形状是．

查看试题解析
15. 如图，在△ABC中，点D为BC边的中点，点E为AC上一点，将∠C沿DE所在直线翻折，使点C落在AB上的点F处．若AC＝10cm，则EF＝cm．

查看试题解析
16. 如图，在△ABC中，已知∠CDE＝64°，∠A＝30°，DE垂直平分BC，则∠ABD的度数为°

查看试题解析
17. 如图，在四边形ACDB中，∠B＝∠D＝90°，CO平分∠ACD，点O为BD的中点．若AB＝2，CD＝4，则AC＝．

查看试题解析
18. 希望小组的同学在求式子 $\frac{1}{2} a + \frac{1}{2^{2}} a + \frac{1}{2^{3}} a + \frac{1}{2^{4}} a + ... + \frac{1}{2^{n}} a$ 的值（结果用 $n$ 和 $a$ 表示）时遇到了困难．经过合作探究他们想出了如图所示的图形来解释这个式子：设△ABC的面积为 $a$ ，取BC的中点，则有△ABD的面积为 $\frac{1}{2} a$ ，再取AD的中点E，则有△ACE的面积为 $\frac{1}{2^{2}} a$ ，再取CE的中点F，则有△DEF的面积为 $\frac{1}{2^{3}} a$ ，……照此思路持续取下去．就可利用这个图形求得 $\frac{1}{2} a + \frac{1}{2^{2}} a + \frac{1}{2^{3}} a + \frac{1}{2^{4}} a + ... + \frac{1}{2^{n}} a$ 的值＝．

查看试题解析

三、解答题

19. 如图，正三角形网格中，已知两个小三角形被涂黑．

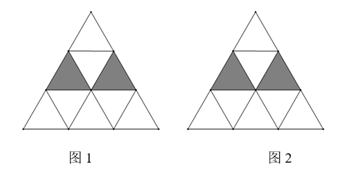(1)、再将图中1其余小三角形涂黑一个，使整个被涂黑的图案构成一个轴对称图形（画出两种不同的）；

(2)、再将图中2其余小三角形涂黑两个，使整个被涂黑的图案构成一个轴对称图形（画出两种不同的）．

查看试题解析
20. 如图，线段AD上有两点E，B，且AE＝DB，分别以AB，DE为直角边在线段AD同侧作Rt△ABC和Rt△DEF，∠A＝∠D＝90°，BC＝EF．求证：∠AEG＝∠DBG．

查看试题解析
21. 如图，在△ABC中，AB＝AC，AD⊥BC于点D．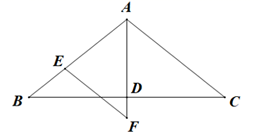

(1)、若∠C＝40°，求∠BAD的度数；

(2)、若点E在边AB上，EF∥AC交AD的延长线于点F，求证：AE=FE．

查看试题解析
22. 如图，在四边形 $A B C D$ 中， $∠ B = ∠ D = 90 °$ ，点E，F分别在 $A B$ ， $A D$ 上， $A E = A F$ ， $C E = C F$ ，求证： $C B = C D$ ．

查看试题解析
23. 如图，已知∠AOB＝60°，E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C，D是垂足，连接CD交OE于点F．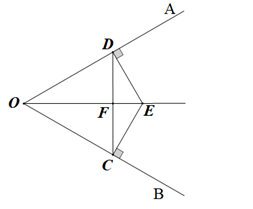

(1)、求证：△OCD是等边三角形；

(2)、若EF＝6，求线段OE的长．

查看试题解析
24. 综合与实践：初步探究：

(1)、如图1，直线 $m$ 同侧有两定点D，E，点A，B，C是直线 $m$ 上的三个动点．在运动过程中，当∠DAB＝∠DBE＝∠BCE＝60°时，求∠D和∠E的数量关系．

(2)、当点A，B，C三个动点运动到如图2所示的位置时，有∠DAB＝∠DBE＝∠BCE＝90°，求此时∠D和∠E的数量关系；若∠DAB＝∠DBE＝∠BCE＝ $α$ 时，∠D和∠E又有什么样的数量关系？（请直接写出这两个问题的答案）

(3)、在图2中，如果∠DAB＝∠DBE＝∠BCE＝90°仍然存在，再添加条件BD＝EB，求证：AC＝AD＋CE．

查看试题解析