山东省临沂市河东区2021-2022学年八年级上学期期中数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若点P(2,3)关于y轴对称点是P1 , 则P1点坐标是( )A、(−3, −2) B、(−2, −3) C、(−2, 3) D、(2, −3)3. 如图,要测量河两岸相对的两点A,B的距离,先在 的垂线 上取两点C,D,使 ,再作出 的垂线 ,使点A,C,E在同一条直线上,可以说明 ,得 ,因此测得 的长就是 的长,判定 ,最恰当的理由是( )
2. 若点P(2,3)关于y轴对称点是P1 , 则P1点坐标是( )A、(−3, −2) B、(−2, −3) C、(−2, 3) D、(2, −3)3. 如图,要测量河两岸相对的两点A,B的距离,先在 的垂线 上取两点C,D,使 ,再作出 的垂线 ,使点A,C,E在同一条直线上,可以说明 ,得 ,因此测得 的长就是 的长,判定 ,最恰当的理由是( ) A、 B、 C、 D、4. 如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条应钉在( )
A、 B、 C、 D、4. 如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条应钉在( )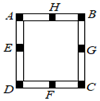 A、E,H两点之间 B、E,G两点之间 C、F,H两点之间 D、A,B两点之间5. 如图,在 中 , 是 的中点, ,则 ( ).
A、E,H两点之间 B、E,G两点之间 C、F,H两点之间 D、A,B两点之间5. 如图,在 中 , 是 的中点, ,则 ( ). A、108° B、72° C、54° D、36°6. 一个多边形的每个内角均为140°,则这个多边形是( )
A、108° B、72° C、54° D、36°6. 一个多边形的每个内角均为140°,则这个多边形是( )
A、七边形 B、八边形 C、九边形 D、十边形7. 小明把一副含 , 角的直角三角板按如图所示的方式摆放,其中 , , ,则 等于( )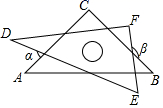 A、 B、 C、 D、8. 请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等的知识,说明画 的依据是( )
A、 B、 C、 D、8. 请仔细观察用直尺和圆规作一个角等于已知角的示意图,请你根据所学的三角形全等的知识,说明画 的依据是( ) A、 B、 C、 D、9. 如图,在 中, , ,分别以点 和点 为圆心,大于 的长为半径画弧,两弧相交于点 , ,作直线 ,交 于点 ,连接 ,则 的度数为( )
A、 B、 C、 D、9. 如图,在 中, , ,分别以点 和点 为圆心,大于 的长为半径画弧,两弧相交于点 , ,作直线 ,交 于点 ,连接 ,则 的度数为( ) A、45° B、55° C、60° D、65°10. 如图,△ABC的面积为12,AB=AC,BC=4,AC的垂直平分线EF分别交AB,AC边于点E,F,若点D为BC边的中点,点P为线段EF上一动点,则△PCD周长的最小值为( )
A、45° B、55° C、60° D、65°10. 如图,△ABC的面积为12,AB=AC,BC=4,AC的垂直平分线EF分别交AB,AC边于点E,F,若点D为BC边的中点,点P为线段EF上一动点,则△PCD周长的最小值为( )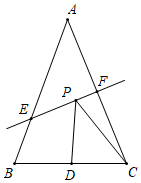 A、6 B、8 C、10 D、1211. 如图为八个全等的正六边形(六条边相等,六个角相等)紧密排列在同一平面上的情形.根据图中标示的各点位置,下列三角形中与△ACD全等的是( )
A、6 B、8 C、10 D、1211. 如图为八个全等的正六边形(六条边相等,六个角相等)紧密排列在同一平面上的情形.根据图中标示的各点位置,下列三角形中与△ACD全等的是( ) A、△ACF B、△AED C、△ABC D、△BCF12. 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,……,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
A、△ACF B、△AED C、△ABC D、△BCF12. 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,……,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )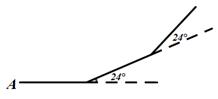 A、140米 B、150米 C、160米 D、240米13. 如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是( )
A、140米 B、150米 C、160米 D、240米13. 如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是( ) A、γ=2α+β B、γ=α+2β C、γ=α+β D、γ=180°﹣α﹣β14. 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )
A、γ=2α+β B、γ=α+2β C、γ=α+β D、γ=180°﹣α﹣β14. 如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )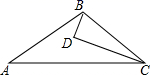 A、1 B、 C、 D、4
A、1 B、 C、 D、4二、填空题
-
15. 等腰三角形的周长为 ,其中一边长为 ,则该等腰三角形的底边长为 .16. 如图,在△ABC中,∠ABC=90°,AC⊥BD,AC=BD,若DE⊥BC,AB=2.8,BC=6,则CE的长为 .
 17. 如图,在△ABC中,已知D,E,F分别为BC,AD,CE的中点,且S△ABC=8cm2 , 则图中阴影部分△BEF的面积等于cm2 .
17. 如图,在△ABC中,已知D,E,F分别为BC,AD,CE的中点,且S△ABC=8cm2 , 则图中阴影部分△BEF的面积等于cm2 . 18. 如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是 .
18. 如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是 . 19. 在△ABC中给定下面几组条件:①AB=4cm,AC=3cm,∠ABC=30°;②AB=3cm,AC=4cm,∠ABC=90°;③AB=3cm,AC=4cm,∠ABC=120°;④AB=3cm,AC=4cm,∠ABC=30°.若根据每组条件画图,则△ABC能够唯一确定的是(填序号).
19. 在△ABC中给定下面几组条件:①AB=4cm,AC=3cm,∠ABC=30°;②AB=3cm,AC=4cm,∠ABC=90°;③AB=3cm,AC=4cm,∠ABC=120°;④AB=3cm,AC=4cm,∠ABC=30°.若根据每组条件画图,则△ABC能够唯一确定的是(填序号).三、解答题
-
20. 如图,已知BD为△ABC的角平分线请按如下要求操作与解答:
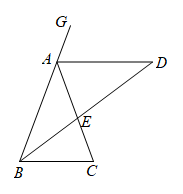
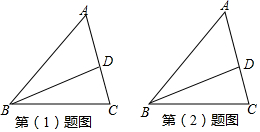 (1)、过点D画DE∥BC交AB于点E.若∠A=68°,∠AED=42°,求△BCD各内角的度数;(2)、画△ABC的角平分线CF交BD于点M,若∠A=60°,请找出图中所有与∠A相等的角,并说明理由.21. 如图,在四边形ABCD中, ,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:
(1)、过点D画DE∥BC交AB于点E.若∠A=68°,∠AED=42°,求△BCD各内角的度数;(2)、画△ABC的角平分线CF交BD于点M,若∠A=60°,请找出图中所有与∠A相等的角,并说明理由.21. 如图,在四边形ABCD中, ,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证: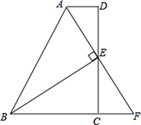 (1)、FC=AD;(2)、AB=BC+AD.22. 如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测得到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,你能计算出塔的高度DE吗?写出计算过程.
(1)、FC=AD;(2)、AB=BC+AD.22. 如图,学校科技小组计划测量一处电信塔的高度,小明在A处用仪器测得到塔尖D的仰角∠DAC=15°,向塔正前方水平直行260m到达点B,测得到塔尖的仰角∠DBC=30°,若小明的眼睛离地面1.6m,你能计算出塔的高度DE吗?写出计算过程. 23. 如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
23. 如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长. 24. 如图,在等边三角形ABC中,点D,E分别在BC,AB上,且BD=AE,AD与CE交于点F
24. 如图,在等边三角形ABC中,点D,E分别在BC,AB上,且BD=AE,AD与CE交于点F (1)、求证:AD=CE;(2)、求∠DFC的度数.
(1)、求证:AD=CE;(2)、求∠DFC的度数.