山东省济南市高新区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2021-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. 9的平方根是（）

A、 -3 B、3 C、±3 D、81

查看试题解析
2. 在平面直角坐标系中，下列各点属于第四象限的是（）

A、 $(1, 2)$ B、 $(- 3, 8)$ C、 $(- 3, - 5)$ D、 $(6, - 7)$

查看试题解析
3. 下列二次根式中是最简二次根式的是（）．

A、 $\sqrt{0.3}$ B、 $\sqrt{7}$ C、 $\sqrt{12}$ D、 $\sqrt{\frac{2}{3}}$

查看试题解析
4. 已知点 $(- 4 ， y_{1}) ， (2 ， y_{2})$ 都在直线 $y = \frac{1}{2} x + 2$ 上，则 $y_{1}$ 和 $y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、无法确定

查看试题解析
5. 下列运算正确的是（）

A、2 $\sqrt{2}$ - $\sqrt{2}$ =1 B、 $\sqrt{6}$ + $\sqrt{3}$ = $\sqrt{9}$ C、 $\sqrt{2}$ × $\sqrt{8}$ =4 D、 $\sqrt{6}$ ÷ $\sqrt{3}$ =2

查看试题解析
6. 已知正比例函数 $y = k x$ 的图象经过点（﹣3，6），则 $k$ 的值是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
7. 小明根据某个一次函数关系式填写了如下的表格：其中有一格不慎被墨汁遮住了，想想看，该空格里原来填的数是（）

$x$

－2

-1

0

1

$y$

6

2

0

A、－2 B、0 C、2 D、4

查看试题解析
8. 已知 $a$ ， $b$ 为两个连续的整数，且 $a < \sqrt{18} < b$ ，则 $a + b$ 的值等于（）

A、7 B、9 C、11 D、13

查看试题解析
9. 如图，数轴上A表示数﹣2，过数轴上表示1的点B作BC⊥x轴，若BC＝2，以A为圆心，AC为半径作圆弧交数轴于点P，那么数轴上点P所表示的数是（）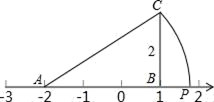

A、 $\sqrt{13}$ B、 $\sqrt{13}$ ﹣2 C、 $\sqrt{13}$ ﹣3 D、4﹣ $\sqrt{13}$

查看试题解析
10. 实数a、b在数轴上对应的位置如图，则 $\sqrt{{(b - 1)}^{2}} - \sqrt{{(a - 1)}^{2}} =$ （）

A、b-a B、2-a-b C、a-b D、2+a-b

查看试题解析
11. 下列图形中，表示一次函数 $y = a x + b$ 与正比例函数 $y = \frac{a x}{b} (a$ ， $b$ 为常数，且 $a b \neq 0)$ 的图象的是（）

A、 B、 C、 D、

查看试题解析
12. 一个容器内有进水管和出水管，开始4min内只进水不出水，在随后的8min内既进水又出水，第12min后只出水不进水.进水管每分钟的进水量和出水量每分钟的出水量始终不变，容器内水量 $y$ （单位：L）与时间 $x$ （单位：min）之间的关系如图所示．

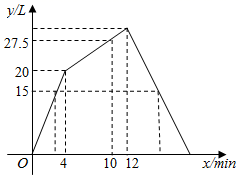
根据图象有下列说法：①进水管每分钟的进水量为5L；② $4 \leq x \leq 12$ 时， $y = \frac{5}{4} x + 15$ ；③当 $x = 12$ 时， $y = 30$ ；④当 $y = 15$ 时， $x = 3$ ，或 $x = 17$ ．其中正确说法的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 在平面直角坐标系中，把点 $(1, - 2)$ 向上平移 $3$ 个单位后的坐标是．

查看试题解析
14. 函数 $y = \sqrt{x - 2}$ 中自变量x的取值范围是．

查看试题解析
15. 已知函数y=（m﹣1）x+m²﹣1是正比例函数，则m=

查看试题解析
16. 已知 $P_{1} (a - 1, 5)$ 和 $P_{2} (2, b - 1)$ 关于x轴对称，则 ${(a + b)}^{2020}$ 值为．

查看试题解析
17. 如图，直线y＝ax+b过点A（0，3）和点B（﹣2，0），则方程ax+b＝0的解是．

查看试题解析
18. 如图，直线y＝2x+2与x轴、y轴分别交于A、B两点，点C是第二象限内一点，△ABC为等腰直角三角形且∠C＝90°，则直线BC的解析式为．

查看试题解析

三、解答题

19. 计算： $\sqrt{27} - \sqrt{12} + \sqrt{\frac{1}{3}}$

查看试题解析
20. 计算： ${(2 + \sqrt{3})}^{2} - (2 + \sqrt{5}) (2 - \sqrt{5})$ ．

查看试题解析
21. 将下列各数填入相应的集合内．
$- \frac{11}{2}$ ， $\sqrt[3]{2}$ ， $\sqrt{4}$ ， $0. \dot{2} \dot{3}$ ， $\sqrt[3]{8}$ ， $- \frac{π}{4}$ ．

(1)、无理数集合： ${$ $\dots}$ ；

(2)、负实数集合： ${$ $\dots}$ ．

查看试题解析
22. 如图所示，在平面直角坐标系中，已知A（0，1），B（2，0），C（4，3）．

(1)、在平面直角坐标系中画出△ABC ，则△ABC的面积是；

(2)、若点D与点C关于原点对称，则点D的坐标为；

(3)、已知P为x轴上一点，若△ABP的面积为4，求点P的坐标．

查看试题解析
23. 某羽毛球馆有两种消费方式：一种是交100元办一张会员卡，以后每次打球费用为25元/小时；另一种是不办会员卡，每次打球费用为40元/小时．

(1)、直接写出办会员卡打球的费用y₁（元）与打球时间x（小时）之间的关系式；

(2)、直接写出不办会员卡打球的费用y₂（元）与打球时间x（小时）之间的关系式；

(3)、小王每月打球时间为10小时，他选用哪种方式更合算？

查看试题解析
24. 在平面直角坐标系中，直线 $y = - 3 x + 2$ 与 $y$ 轴交于点 $C$ ，直线 $y = x + b (b \neq 0)$ 与 $y$ 轴交于点 $A$ ，与直线 $y = - 3 x + 2$ 交于点 $B$ ，设点 $B$ 的横坐标为-2．

(1)、求点 $B$ 的坐标及 $b$ 的值；

(2)、根据图象直接写出不等式 $- 3 x + 2 > x + b$ 的解集；

(3)、点 $P$ 为 $x$ 轴上一点，当 $| P A - P B |$ 最大时，求点 $P$ 的坐标．

查看试题解析
25. 观察下列一组式子的变形过程，然后回答问题：
例1： $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{{(\sqrt{2})}^{2} - 1} = \frac{\sqrt{2} - 1}{1} = \sqrt{2} - 1$ ．

例2： $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}} = \sqrt{4} - \sqrt{3}$ $\dots$

(1)、化简： $\frac{1}{\sqrt{6} + \sqrt{5}} =$ ；

(2)、观察上面的解题过程，请你猜想一规律：直接写出式子 $\frac{1}{\sqrt{n} + \sqrt{n - 1}} =$ ；

(3)、利用这一规律计算： $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \dots + \frac{1}{\sqrt{2020} + \sqrt{2019}}) (\sqrt{2020} + 1)$ ．

查看试题解析
26. $A$ ， $B$ 两地相距12千米，甲骑自行车从 $A$ 地出发前往 $B$ 地，同时乙步行从 $B$ 地出发前往 $A$ 地，如图的折线 $O P Q$ 和线段 $E F$ ，分别表示甲、乙两人与 $A$ 地的距离 $y_{甲}$ 、 $y_{乙}$ 与他们所行时间 $x (h)$ 之间的函数关系，且 $O P$ 与 $E F$ 相交于点 $M$ ．

(1)、求 $y_{乙}$ 与 $x$ 的函数关系式以及两人相遇地点与 $A$ 地的距离；

(2)、求线段 $O P$ 对应的 $y_{甲}$ 与 $x$ 的函数关系式；

(3)、求经过多少小时，甲、乙两人相距5千米．

查看试题解析
27. 如图，在平面直角坐标系中，直线 $l_{1}$ 的解析式为 $y = x$ ，直线 $l_{2}$ 的解析式为 $y = - \frac{1}{2} x + 3$ ，与 $x$ 轴、 $y$ 轴分别交于点 $A$ 、点 $B$ ，直线 $l_{1}$ 与 $l_{2}$ 交于点 $C$ ．

(1)、求出点 $A$ 、点 $B$ 的坐标；

(2)、求 $Δ C O B$ 的面积；

(3)、在 $y$ 轴右侧有一动直线平行于 $y$ 轴，分别于 $l_{1}$ 、 $l_{2}$ 交于点 $M$ 、 $N$ ，且点 $M$ 在点 $N$ 的下方， $y$ 轴上是否存在点 $Q$ ，使 $Δ M N Q$ 为等腰直角三角形？若存在，请直接写出满足条件的点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析

$x$	－2	-1	0	1
$y$	6		2	0