河北省唐山市迁安市2021-2022学年八年级上学期期中数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
1. 25的算术平方根是A、5 B、±5 C、-5 D、252. 下列各式中,计算正确的是( )A、 =4 B、 =±5 C、 =1 D、 =±53. 在- ,-2, ,3.14, ,( )2中无理数的个数是( )A、1个 B、2个 C、3个 D、4个4. 如图,AC、BD相交于O,∠1=∠2,若用“SAS”说明 ,则还需加上条件( )
 A、AD=BC B、∠D=∠C C、OA=AB D、BD=AC5. 若分式 的值为零,则x的值为( )A、-1 B、2 C、-2 D、2或-26.6. 近似数1.20是由a四舍五入得到的,那么a的取值范围是A、 B、 C、 D、7. 用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是( )A、SAS B、ASA C、AAS D、8. 下列计算正确的是( )A、 ﹣ = B、3 ×2 =6 C、(2 )2=16 D、 =19. 把分式 中的x、y都扩大3倍,则分式的值( ).A、扩大3倍 B、扩大6倍 C、缩小为原来的 D、不变10. 边长是m的正方形面积是7,如图,表示m的点在数轴上位于哪两个字母之间( )
A、AD=BC B、∠D=∠C C、OA=AB D、BD=AC5. 若分式 的值为零,则x的值为( )A、-1 B、2 C、-2 D、2或-26.6. 近似数1.20是由a四舍五入得到的,那么a的取值范围是A、 B、 C、 D、7. 用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是( )A、SAS B、ASA C、AAS D、8. 下列计算正确的是( )A、 ﹣ = B、3 ×2 =6 C、(2 )2=16 D、 =19. 把分式 中的x、y都扩大3倍,则分式的值( ).A、扩大3倍 B、扩大6倍 C、缩小为原来的 D、不变10. 边长是m的正方形面积是7,如图,表示m的点在数轴上位于哪两个字母之间( ) A、C与D B、A与B C、A与C D、B与C11. 如图,已知AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,则∠CAE的度数为( )
A、C与D B、A与B C、A与C D、B与C11. 如图,已知AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,则∠CAE的度数为( )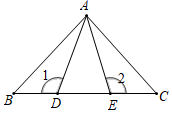 A、20° B、30° C、40° D、50°12. 化简 的结果是( )A、 B、 C、 D、13.
A、20° B、30° C、40° D、50°12. 化简 的结果是( )A、 B、 C、 D、13.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
 A、4个 B、3个 C、2个 D、1个14. 若关于x的分式方程 + =2有增根,则m的值是( )A、m=﹣1 B、m=0 C、m=3 D、m=0或m=315. 某单位向一所希望小学赠送1080件文具,现用A、B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个.设B型包装箱每个可以装x件文具,根据题意列方程为( )A、 B、 C、 D、16. 如图,△ABC中,∠ACB=90°,D为AB上任一点,过D作AB的垂线,分别交边AC、BC的延长线于EF两点,∠BAC∠BFD的平分线交于点I,AI交DF于点M,FI交AC于点N,连接BI.下列结论:①∠BAC=∠BFD;②∠ENI=∠EMI;③AI⊥FI;④∠ABI=∠FBI;其中正确结论的个数是( )
A、4个 B、3个 C、2个 D、1个14. 若关于x的分式方程 + =2有增根,则m的值是( )A、m=﹣1 B、m=0 C、m=3 D、m=0或m=315. 某单位向一所希望小学赠送1080件文具,现用A、B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个.设B型包装箱每个可以装x件文具,根据题意列方程为( )A、 B、 C、 D、16. 如图,△ABC中,∠ACB=90°,D为AB上任一点,过D作AB的垂线,分别交边AC、BC的延长线于EF两点,∠BAC∠BFD的平分线交于点I,AI交DF于点M,FI交AC于点N,连接BI.下列结论:①∠BAC=∠BFD;②∠ENI=∠EMI;③AI⊥FI;④∠ABI=∠FBI;其中正确结论的个数是( )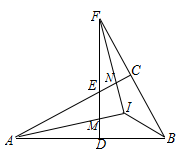 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
17. 在2 , ,0,- ,-0.6这五个数,最大的是18. 如图,一只蚂蚁从点 沿数轴向右爬2个单位到达点 ,点 表示 ,则 表示的数为 .
 19. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为秒时,△ABP和△DCE全等.
19. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为秒时,△ABP和△DCE全等.
三、解答题
-
20.(1)、计算∶(1- )(2)、解方程:21.(1)、化简并求值∶已知x=-3,y=2,求( )÷ 的值.(2)、已知一个正数的两个不相等的平方根是a+6与 2a-9.
①求a的值及这个正数;
②求关于x的方程 ax3-(-8)2=0 的解.
22. 如图,在△ACD中,E为边CD上一点,F为AD的中点,过点A作AB∥CD , 交EF的延长线于点B . (1)、求证:△AFB≌△DFE;(2)、若AB=6,DC=4CE , 求CD的长.23. 课本指出:公认的真命题称为基本事实,除了基本事实外,其他的真命题(如推论、定理等)的符合题意性都需要借助基本事实,通过推理的方法证实.例如:我们学过三角形全等的基本事实有三个,即:“ ”、“ ”、“ ”,请你完成以下问题:(1)、叙述三角形全等的判定方法中的推论 :如果两个三角形的及其中一个对应相等,那么这两个三角形全等.(2)、小红同学对这个推论的符合题意性进行了证明,她画出了 和 ,并写出了如下不完整的已知和求证:
(1)、求证:△AFB≌△DFE;(2)、若AB=6,DC=4CE , 求CD的长.23. 课本指出:公认的真命题称为基本事实,除了基本事实外,其他的真命题(如推论、定理等)的符合题意性都需要借助基本事实,通过推理的方法证实.例如:我们学过三角形全等的基本事实有三个,即:“ ”、“ ”、“ ”,请你完成以下问题:(1)、叙述三角形全等的判定方法中的推论 :如果两个三角形的及其中一个对应相等,那么这两个三角形全等.(2)、小红同学对这个推论的符合题意性进行了证明,她画出了 和 ,并写出了如下不完整的已知和求证:已知:如图, 和 中,
, ,
求证:
(3)、按小红的想法写出证明:
证明:
24. 甲、乙两个工程队计划参与一项工程建设,甲队单独施工20天完成该项工程的 ,这时乙队加入,两队还需同时施工16天,才能完成该项工程.(1)、若甲队单独施工,需要天才能完成任务.(2)、若乙队单独施工,需要多少天才能完成该项工程?(3)、若甲队参与该项工程施工的时间不超过30天,则乙队至少施工多少天才能完成该项工程?25. 已知 中, , ,点D为直线BC上的一动点 点D不与点B、C重合 ,以AD为边作 ,使 , ,连接CE.
发现问题:
如图1,当点D在边BC上时,
(1)、请写出BD和CE之间的位置关系为 , 并猜想BC和CE、CD之间的数量关系: .(2)、如图2,当点D在边BC的延长线上且其他条件不变时, 中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立?若成立,请证明;若不成立,请写出新的数量关系,说明理由;(3)、如图3,当点D在边CB的延长线上且其他条件不变时,若 , ,求线段ED的长.