广东省揭阳市普宁市三校期中联考2021-2022学年八年级上学期期中数学试题

试卷更新日期：2021-11-24 类型：期中考试

进入出卷网下载

一、单选题

1. 下面说法中，正确的是（）

A、实数分为正实数和负实数 B、带根号的数都是无理数 C、无限不循环小数都是无理数 D、平方根等于本身的数是1和0

查看试题解析
2. 如图所示是在方格纸上画出的小旗图案，若用(0，0)表示C点，(-3，2)表示B点，那么A点的位置可表示为（）

A、(0，-3) B、(2，-3) C、(-3，-2) D、(-3，0)

查看试题解析
3. 在△ABC中，AB=12，BC=16，AC=20，则△ABC的面积为（）

A、96 B、120 C、160 D、200

查看试题解析
4. 若一个正数的两个平方根为 $a + 1$ 和 $2 a - 7$ ，则这个正数是（）

A、2 B、3 C、8 D、9

查看试题解析
5. 在平面直角坐标系中，若点P(a－3，1)与点Q(2，b＋1)关于x轴对称，则a＋b的值是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 有理数a和b在数轴上的位置如图所示，则 $\sqrt{b^{2}}$ -∣a-b∣等于（）

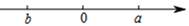A、a B、-a C、2b+a D、2b-a

查看试题解析
7. 如图，分别以 $Rt △ ABC$ 的三边为斜边向外作等腰直角三角形，若斜边 $A B = 6$ ，则图中阴影部分的面积为（）．

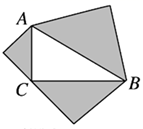A、6 B、12 C、16 D、18

查看试题解析
8.
如图，边长均为1个单位的正方形组成的方格纸内有一张笑脸图案，已知左眼的坐标是（﹣1，0），那么右眼关于鼻子所在的水平线对称的点的坐标是（　　）

A、（1，﹣2） B、（1，﹣1） C、（﹣1，0） D、（﹣1，﹣2）

查看试题解析
9. 如图， $△ A B C$ 中， $∠ A C B = 90 ° ， A C = 8 ， B C = 6$ ，将 $△ A D E$ 沿DE翻折，使点A与点B重合，则CE的长为（）

A、 $\frac{19}{8}$ B、2 C、 $\frac{25}{4}$ D、 $\frac{7}{4}$

查看试题解析
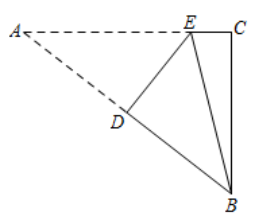10. 如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△ $A_{1} B_{1} C_{1}$ 的位置，点B，O分别落在点B₁、C₁处，点B₁在x轴上，再将△ $A_{1} B_{1} C_{1}$ 绕点B₁顺时针旋转到△ $A_{1} B_{1} C_{2}$ 的位置，点C₂在x轴上，将△ $A_{1} B_{1} C_{2}$ 绕点C₂顺时针旋转到△ $A_{2} B_{2} C_{2}$ 的位置，点A₂在x轴上，依次进行下去…．若点A( $\frac{5}{3}$ ，0)，B(0，4)，则点 $B_{2019}$ 的横坐标（）

A、10096 B、10097 C、10098 D、10020

查看试题解析

二、填空题

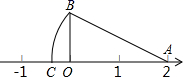
11. 如图数轴上的点O表示的数是0，点A表示的数是2， $O B ⊥ O A$ ，垂足为O，且 $O B = 1$ ，以A为圆心， $A B$ 长为半径画弧，交数轴于点C，则点C表示的数为.

查看试题解析
12. a是 $\sqrt{13}$ 的整数部分，b是 $\sqrt{13}$ 的小数部分，则 $3 a - b =$ ；

查看试题解析
13. 如图，所有阴影部分四边形都是正方形，所有三角形都是直角三角形，若正方形A、C、D的面积依次为4、6、18，则正方形B的面积为.

查看试题解析
14. 已知点P的坐标为(3-2a，a-9)，且点P到两坐标轴的距离相等，则点P的坐标为

查看试题解析
15. 若 $\sqrt{a - 3} - 2 \sqrt{3 - a} = b + 6$ ，则a-b的算术平方根为．

查看试题解析
16. 如图，圆柱形无盖玻璃容器，高18cm，底面周长为60cm，在外侧距下底1cm的点C处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇，则急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度为cm（容器壁厚度忽略不计）．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{18}$ ﹣ $\sqrt{32} + \sqrt{2}$

(2)、（ $\sqrt{5} + 2$ ）（ $\sqrt{5} - 2$ ）﹣（ $\sqrt{3}$ ）² ．

查看试题解析
18. 如图，在平面直角坐标系中，△ABC的顶点A，B，C均在正方形网格的格点上.

(1)、画出△ABC关于y轴的对称图形△A₁B₁C₁；

(2)、直接写出△A₁B₁C₁各个顶点的坐标.

查看试题解析
19. 阅读下列材料，然后解答下列问题：
在进行代数式化简时，我们有时会碰上如 $\frac{5}{\sqrt{3}}$ ， $\frac{2}{\sqrt{3} + 1}$ 这样的式子，其实我们还可以将其进一步化简：

(一) $\frac{5}{\sqrt{3}} = \frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{5 \sqrt{3}}{3}$ ；

(二) $\frac{2}{\sqrt{3} + 1} = \frac{2 （ \sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \sqrt{3} - 1$ ；

(三) $\frac{2}{\sqrt{3} + 1} = \frac{3 - 1}{\sqrt{3} + 1} = \frac{{(\sqrt{3})}^{2} - 1^{2}}{\sqrt{3} + 1} = \frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1} = \sqrt{3} - 1$ .

以上这种化简的方法叫分母有理化.

(1)、请用不同的方法化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ：
①参照(二)式化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ＝.

②参照(三)式化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ＝__

(2)、化简： $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + \dots + \frac{1}{\sqrt{99} + \sqrt{97}}$ .

查看试题解析
20. 如图，已知等腰△ABC的底边BC＝13，D是腰AB上一点，且CD＝12，BD＝5．

(1)、求证：△BDC是直角三角形；

(2)、求AC的长．

查看试题解析
21. 在平面直角坐标系中，已知点A(8，0)，点B(3，0)，点C是点A关于点B的对称点

(1)、求点C的坐标；

(2)、如果点P在y轴上，过点P作直线l∥x轴，点A关于直线l的对称点是点D，当△BCD的面积等于10时，求点P的坐标．

查看试题解析
22. 如图，将一张长方形纸片 $A B C D$ 沿 $E$ 折叠，使 $C ， A$ 两点重合．点 $D$ 落在点 $G$ 处．已知 $A B =4$ ， $B C = 8$ ．

(1)、求证： $Δ A E F$ 是等腰三角形；

(2)、求线段 $F D$ 的长．

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点D是 $B C$ 上一动点，连接 $A D$ ，过点A作 $A E ⊥ A D$ ，并且始终保持 $A E = A D$ ，连接 $C E$ .

(1)、求证： $△ A B D ≌ △ A C E$ ；

(2)、若 $A F$ 平分 $∠ D A E$ 交 $B C$ 于F，若 $B D = 3$ ， $C F = 4$ ，求 $D F$ 的长.

查看试题解析