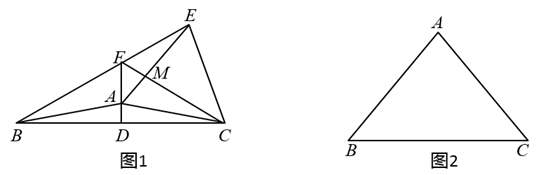广东省广州市2021-2022学年八年级上学期期中数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
1. 盖房子时,木工师傅常常先在窗框上斜钉一根木条,利用的几何原理是( )A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短2. 一个八边形的内角和度数为( )A、360° B、720° C、900° D、1080°3. 已知a、b、c为三角形的三边,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是( )A、0 B、2a C、2(b﹣c) D、2(a+c)4. 在下列说法中,正确的是( )
A、如果两个三角形全等,则它们必是关于直线成轴对称的图形 B、如果两个三角形关于某直线成轴对称,那么它们是全等三角形 C、等腰三角形是关于底边中线成轴对称的图形 D、一条线段是关于经过该线段中点的直线成轴对称的图形5. 如图, , , , 恒满足的关系式是( ) A、 B、 C、 D、6. 等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为( )A、65° B、105° C、55°或105° D、65°或115°7. 如图,AB//DE,AC//DF,AC=DF,下列条件中,不能判定△ABC≌△DEF的是( )
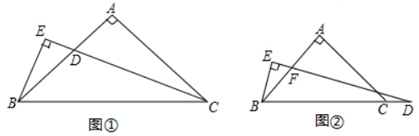
A、 B、 C、 D、6. 等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为( )A、65° B、105° C、55°或105° D、65°或115°7. 如图,AB//DE,AC//DF,AC=DF,下列条件中,不能判定△ABC≌△DEF的是( )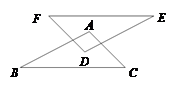 A、AB=DE B、∠B=∠E C、EF=BC D、EF//BC8. 如图,三角形纸片 中, , ,将 沿 对折,使点 落在 外的点 处,若 ,则 的度数是( )
A、AB=DE B、∠B=∠E C、EF=BC D、EF//BC8. 如图,三角形纸片 中, , ,将 沿 对折,使点 落在 外的点 处,若 ,则 的度数是( ) A、 B、 C、 D、9. 如图,△ABC≌△AED,点E在线段BC上,∠1=40°,则∠AED的度数是( )
A、 B、 C、 D、9. 如图,△ABC≌△AED,点E在线段BC上,∠1=40°,则∠AED的度数是( ) A、70° B、68° C、65° D、60°10. 如图,∠AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是边OB、OA上的动点,记∠MPQ= ,∠PQN= ,当MP+PQ+QN最小时,则 的值为( )
A、70° B、68° C、65° D、60°10. 如图,∠AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是边OB、OA上的动点,记∠MPQ= ,∠PQN= ,当MP+PQ+QN最小时,则 的值为( ) A、10° B、20° C、40° D、60°
A、10° B、20° C、40° D、60°二、填空题
-
11. 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .12. 把一块直尺与一块直角三角板如图放置,若 ,则 的度数为 .
 13. 已知△ABC的三边长分别为a,b,c,且a,b满足 ,则c 的取值范围是 .14. 已知直角坐标系中点 和点B(3,b)关于x轴对称,则b-a= .15. 如图, , 是 延长线上的一点, ,动点 从点 出发沿 以 的速度移动,动点 从点 发沿 以 的速度移动,如果点 同时出发,用 表示移动的时间,当 时, 是等腰三角形.
13. 已知△ABC的三边长分别为a,b,c,且a,b满足 ,则c 的取值范围是 .14. 已知直角坐标系中点 和点B(3,b)关于x轴对称,则b-a= .15. 如图, , 是 延长线上的一点, ,动点 从点 出发沿 以 的速度移动,动点 从点 发沿 以 的速度移动,如果点 同时出发,用 表示移动的时间,当 时, 是等腰三角形. 16. 如图,在 中, 和 的平分线 、 相交于点 , 交 于点 , 交 于点 ,过点 作 于点 ,则下列三个结论:① ;②当 时, ;③若 , ,则 .其中正确的是 .
16. 如图,在 中, 和 的平分线 、 相交于点 , 交 于点 , 交 于点 ,过点 作 于点 ,则下列三个结论:① ;②当 时, ;③若 , ,则 .其中正确的是 .
三、解答题
-
17. 四边形 中,四个内角度数之比是 ,求出四个内角的度数.18. 如图,在 和 中, , , ,求 的度数.
 19. 如图,已知AE⊥BC,AD平分∠BAE,∠ADB=110°,∠CAE=20°,求∠BAC和∠B的度数.
19. 如图,已知AE⊥BC,AD平分∠BAE,∠ADB=110°,∠CAE=20°,求∠BAC和∠B的度数. 20. 如图,已知:在△ABC中,AB=AC,∠BAC=120°,D为BC边的中点,DE⊥AC.求证:CE=3AE.
20. 如图,已知:在△ABC中,AB=AC,∠BAC=120°,D为BC边的中点,DE⊥AC.求证:CE=3AE. 21. 如图,在平面直角坐标系中, 的三个顶点均在格点上,
21. 如图,在平面直角坐标系中, 的三个顶点均在格点上,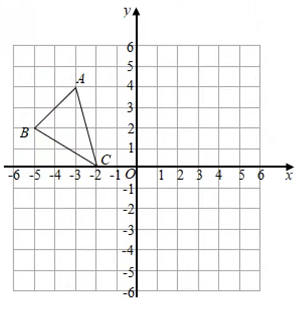 (1)、在网格中作出 关于 轴对称的图形 ;(2)、直接写出 、 、 的坐标;(3)、若网格的单位长度为 ,求 的面积.22. 已知:如图,在△ABC中,∠ACB=90°,∠A=30°.求证:BC= AB.
(1)、在网格中作出 关于 轴对称的图形 ;(2)、直接写出 、 、 的坐标;(3)、若网格的单位长度为 ,求 的面积.22. 已知:如图,在△ABC中,∠ACB=90°,∠A=30°.求证:BC= AB. 23. 已知等边三角形 ,
23. 已知等边三角形 , (1)、尺规作图:过顶点 、 、 依次作 、 、 的垂线,三条垂线交于点 、 、 (保留一条垂线的作图痕迹,另两条垂线的作图痕迹可以不保留,不需要写作法)(2)、求证: 是等边三角形.
(1)、尺规作图:过顶点 、 、 依次作 、 、 的垂线,三条垂线交于点 、 、 (保留一条垂线的作图痕迹,另两条垂线的作图痕迹可以不保留,不需要写作法)(2)、求证: 是等边三角形.