安徽省宿州市埇桥区教育集团2021-2022学年八年级上学期期中考试数学试题
试卷更新日期:2021-11-24 类型:期中考试
一、单选题
-
1. 在实数 中,最小的数是( )A、 B、0 C、-1 D、2. 在平面直角坐标系中,点 在x轴上,则m的值为( )A、-2 B、-1 C、1 D、33. 已知a,b,c是三角形的三边,若满足 ,则该三角形的形状是( )A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形4. 若将三个数- , , 表示在数轴上,其中能被如图所示的墨迹覆盖的数是( )
 A、- B、 C、 D、无法确定5. 如图,象棋盘上,若“将”位于点(3,﹣2),“车”位于点(﹣1,﹣2),则“马”位于( )
A、- B、 C、 D、无法确定5. 如图,象棋盘上,若“将”位于点(3,﹣2),“车”位于点(﹣1,﹣2),则“马”位于( )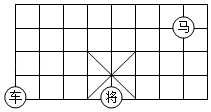 A、(1,3) B、(5,3) C、(6,1) D、(8,2)6. 下列运算正确的是( )A、 B、 C、 D、7. 对于函数 ,下列说法正确的是( )A、图象经过点 B、y随着x的增大而增大 C、图象与x轴交于点 D、图象不经过第三象限8. 一次函数y=mx+n与y=mnx(mn≠0),在同一平面直角坐标系的图象是( )A、
A、(1,3) B、(5,3) C、(6,1) D、(8,2)6. 下列运算正确的是( )A、 B、 C、 D、7. 对于函数 ,下列说法正确的是( )A、图象经过点 B、y随着x的增大而增大 C、图象与x轴交于点 D、图象不经过第三象限8. 一次函数y=mx+n与y=mnx(mn≠0),在同一平面直角坐标系的图象是( )A、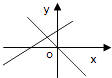 B、
B、 C、
C、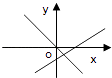 D、
D、 9. 汽车由A地驶往相距120 km的B地,它的平均速度是30 km/h,则汽车距B地的路程s(km)与行驶时间t(h)的函数关系式及自变量t的取值范围是( )A、s=120-30t(0≤t≤4) B、s=120-30t(t>0) C、s=30t(0≤t≤4) D、s=30t(t<4)10. 在直线l上依次摆放着七个正方形.如图,已知斜放置的三个正方形的面积分别为1,2,3.正放置的四个正方形的面积依次是 , , , ,则 的值为( )
9. 汽车由A地驶往相距120 km的B地,它的平均速度是30 km/h,则汽车距B地的路程s(km)与行驶时间t(h)的函数关系式及自变量t的取值范围是( )A、s=120-30t(0≤t≤4) B、s=120-30t(t>0) C、s=30t(0≤t≤4) D、s=30t(t<4)10. 在直线l上依次摆放着七个正方形.如图,已知斜放置的三个正方形的面积分别为1,2,3.正放置的四个正方形的面积依次是 , , , ,则 的值为( ) A、4 B、6 C、8 D、
A、4 B、6 C、8 D、二、填空题
-
11. 的平方根是 .12. 若点A(m+2,3)与点B(﹣4,n+5)关于x轴对称,则m+n=.13. 如图是“俄罗斯方块”游戏中的一个图案,由四个完全相同的小正方形拼成,则∠ABC的度数为 .
 14. 将直线 向上平移3个单位,所得直线的表达式为.15. 如图,长方体的底面边长分别为 和 ,高为 .若一只蚂蚁从 点开始经过4个侧面爬行一圈到达 点,则蚂蚁爬行的最短路径的长度是cm.
14. 将直线 向上平移3个单位,所得直线的表达式为.15. 如图,长方体的底面边长分别为 和 ,高为 .若一只蚂蚁从 点开始经过4个侧面爬行一圈到达 点,则蚂蚁爬行的最短路径的长度是cm. 16. 将 按右侧方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,7)表示的两数之积是 .
16. 将 按右侧方式排列.若规定(m,n)表示第m排从左向右第n个数,则(5,4)与(15,7)表示的两数之积是 .
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 已知点P(m+2,3),Q(−5,n−1),根据以下条件确定m、n的值(1)、P、Q两点在第一、三象限的角平分线上;(2)、PQ∥x轴,且P点与Q点的距离为3.19. 如图,在直角坐标系中, .
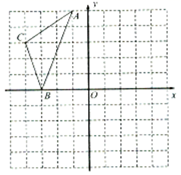 (1)、在图中作出 关于 轴对称的图形 ;(2)、写出点 的坐标.20. 已知,如图所示的一块地,已知AD=12米,CD=9米,∠ADC=90°,AB=39米,BC=36米,求这块地的面积.
(1)、在图中作出 关于 轴对称的图形 ;(2)、写出点 的坐标.20. 已知,如图所示的一块地,已知AD=12米,CD=9米,∠ADC=90°,AB=39米,BC=36米,求这块地的面积.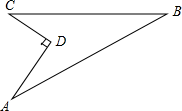 21. 如图
21. 如图 (1)、在图中同一直角坐标系内画出① ,② ,③ ,④ 的图象;(2)、图中四个函数中随着x值的增大,y的值分别如何变化?(3)、直线 与 的位置关系如何?(4)、直线 与直线 有什么共同点?22. 大家知道 是无理数,而无理数是无限不循环小数,因为 ,所以 的整数部分是1, 就是小数部分.
(1)、在图中同一直角坐标系内画出① ,② ,③ ,④ 的图象;(2)、图中四个函数中随着x值的增大,y的值分别如何变化?(3)、直线 与 的位置关系如何?(4)、直线 与直线 有什么共同点?22. 大家知道 是无理数,而无理数是无限不循环小数,因为 ,所以 的整数部分是1, 就是小数部分.请据此解答:
(1)、 的整数部分是 , 小数部分是;(2)、如果 的小数部分为a, 的整数部分为b,求 的值;(3)、若设 的整数部分为x,小数部分为y,求 的值.23. 如图,将一张长方形纸片 放在直角坐标系中,使得 与x轴重合, 与y轴重合,点D为 边上的一点(不与点A、点B重合),且点 ,点 . (1)、如图1,折叠 ,使得点B的对应点 落在对角线AC上,折痕为CD,求此刻点D的坐标.(2)、如图2,折叠 ,使得点A与点C重合,折痕交AB于D点,交AC于点E,求BD.
(1)、如图1,折叠 ,使得点B的对应点 落在对角线AC上,折痕为CD,求此刻点D的坐标.(2)、如图2,折叠 ,使得点A与点C重合,折痕交AB于D点,交AC于点E,求BD.