浙江省绍兴市越清崧联盟2021-2022学年高一上学期期中联考数学试题
试卷更新日期:2021-11-23 类型:期中考试
一、单选题
-
1. 若集合 ,则下面结论正确的是( )A、 B、 C、 D、2. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,3. 已知函数 是 上的偶函数,当 时, ,且 ,则 ( )A、-1 B、0 C、1 D、24. 已知集合A={x|-2≤-x+1<3},B={x|x2-2x-3≤0},则用韦恩图表示它们之间的关系正确的是( )A、
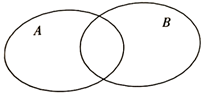 B、
B、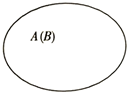 C、
C、 D、
D、 5. 已知 是一次函数,且 ,则 的解析式为( )A、 B、 C、 D、6. “ "是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件7. 定义在实数 上的偶函数 在区间 上单调递减,且 ,则不等式 的解集为( )A、 B、 C、 D、8. 已知两个正实数 满足 ,并且 恒成立,则实数m的取值范围( )A、 B、 C、 D、
5. 已知 是一次函数,且 ,则 的解析式为( )A、 B、 C、 D、6. “ "是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件7. 定义在实数 上的偶函数 在区间 上单调递减,且 ,则不等式 的解集为( )A、 B、 C、 D、8. 已知两个正实数 满足 ,并且 恒成立,则实数m的取值范围( )A、 B、 C、 D、二、多选题
-
9. 已知 ,则下列结论正确的是( )A、 B、 C、 D、10. 关于函数 的描述错误的命题是( )A、 , B、 , C、 , , D、 , ,11. 符号 表示不超过 的最大整数,如 , , ,定义函数 ,以下结论正确的是( )A、函数 的定义域是R,值域为 B、方程 有无数个解 C、函数 是奇函数 D、函数 是增函数.12. 定义在 上的函数 满足 ,当 时, ,则函数 满足( )A、 B、 为奇函数 C、 在区间 上有最小值 D、 的解集为
三、填空题
-
13. 函数 的定义域是 .14. 计算: .15. 已知函数 在 上单调递增,则a的取值范围为.16. 已知 , ,且 ,则 的最小值是.
四、解答题
-
17. 已知集合 ,集合 ,求:(1)、 ;(2)、 ;(3)、 .18. 已知函数(1)、若函数 的图象过点 .求实数m的值,并证明函数 为奇函数;(2)、若 ,用单调性的定义证明函数 在 上单调递增.19. 有一种新型的洗衣液,去污速度特别快,已知每投放 个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度y(克/升)随着时间x(分钟)变化的函数关系式近似为 ,其中 根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.(1)、若只投放一次k个单位的洗衣液,两分钟时水中洗衣液的浓度为3(克/升),求k的值:(2)、若只投放一次4个单位的洗衣液,则有效去污时间可达几分钟?