天津市河北区2021-2022学年高一上学期数学期中考试试卷
试卷更新日期:2021-11-23 类型:期中考试
一、单选题
-
1. 设 , ,则 的结果为( )A、 B、 C、 D、2. 已知集合 ,集合 满足 ,则集合 的个数为( )A、2 B、3 C、4 D、53. 函数 , 的奇偶性是( )A、奇函数 B、偶函数 C、非奇非偶函数 D、既是奇函数又是偶函数4. 已知 : ; : ,那么 是 的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 函数f(x)= 的定义域为( )A、[1,2)∪(2,+∞) B、(1,+∞) C、[1,2) D、[1,+∞)6. 命题“ ”的否定是( )A、 B、 C、 D、7. 已知幂函数 在第一象限内的图象如图所示.若 则与曲线 , , , 对应的n的值依次为( )
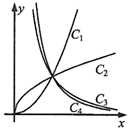 A、 B、 C、 D、8. 已知 为正实数,且 ,则 的最大值为( )A、1 B、2 C、 D、9. 如果关于 的不等式 的解集是 ,那么 等于( )A、-81 B、81 C、-64 D、6410. 不等式 对于一切实数恒成立,则k的取值范围为( )A、 B、 C、 D、
A、 B、 C、 D、8. 已知 为正实数,且 ,则 的最大值为( )A、1 B、2 C、 D、9. 如果关于 的不等式 的解集是 ,那么 等于( )A、-81 B、81 C、-64 D、6410. 不等式 对于一切实数恒成立,则k的取值范围为( )A、 B、 C、 D、二、填空题
-
11. 函数 , 的单调递增区间是;单调递减区间是.12. 化简 .13. 不等式 的解集是.14. 集合 用列举法表示是.15. 下列命题中为真命题的是.(填写序号)
①若 ,则 ;②若 ,则 ;③若 且 ,则 ;④若 且 .则
16. 函数 满足 的 的取值范围是.三、解答题
-
17. 设集合 , .(1)、若 ,试判断集合 与 的关系;(2)、若 ,求实数 的取值集合.18. 已知函数 ( 且 )在 上最大值是最小值的2倍,求实数 的值.
