江苏省无锡市滨湖区2021-2022学年高一上学期数学期中考试试卷
试卷更新日期:2021-11-23 类型:期中考试
一、单选题
-
1. 集合 中的元素个数有( )A、1 B、2 C、3 D、42. 已知幂函数 的图象过点 ,则 ( )A、 B、 C、4 D、3. 如果 ,那么下列不等式中正确的是( )A、 B、 C、 D、4. “ 且 ”是“ ”成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、即不充分也不必要条件5. 函数 的图象大致为( )A、
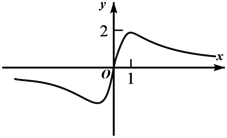 B、
B、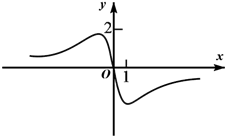 C、
C、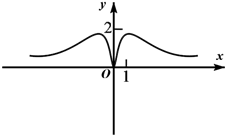 D、
D、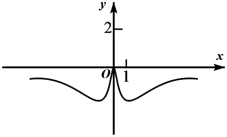 6. 如图所示,矩形ABCD的边AB靠在墙PQ上,另外三边是由篱笆围成的.若该矩形的面积为4,则围成矩形ABCD所需要篱笆的( )
6. 如图所示,矩形ABCD的边AB靠在墙PQ上,另外三边是由篱笆围成的.若该矩形的面积为4,则围成矩形ABCD所需要篱笆的( ) A、最小长度为8 B、最小长度为 C、最大长度为8 D、最大长度为7. 已知偶函数 在 上单调递增,且 ,则满足 的x的取值范围是( )A、 B、 C、 D、8. 若函数 是 上的减函数,则实数 的取值范围是( )A、 B、 C、 D、
A、最小长度为8 B、最小长度为 C、最大长度为8 D、最大长度为7. 已知偶函数 在 上单调递增,且 ,则满足 的x的取值范围是( )A、 B、 C、 D、8. 若函数 是 上的减函数,则实数 的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 设全集 ,集合 ,则( )A、 B、 C、 D、集合A的真子集个数为810. 已知 且 ,那么下列不等式中,恒成立的有( )A、 B、 C、 D、11. 下列各结论中正确的是( )A、“ ”是“ ”的充要条件 B、“ ”的最小值为 C、命题“ , ”的否定是“ , ” D、“ ”是“ ”的充分不必要条件12. 对任意两个实数 ,定义 ,若 , ,下列关于函数 的说法正确的是( )A、函数 是偶函数 B、方程 有两个解 C、方程 至少有三个根 D、函数 有最大值为0,无最小值
三、填空题
-
13. 函数 的定义域为.14. 已知函数 ,则 .15. 已知函数 ,则函数 的最大值为.16. 已知函数 是定义在 的奇函数,则实数 的值为;若函数 ,如果对于 , ,使得 ,则实数 的取值范围是.
四、解答题
-
17. 已知集合 或 , .(1)、求 ;(2)、求 .18. 已知函数 .
 (1)、求 的值;(2)、画出函数 的图象;(3)、指出函数 的单调区间.(直接写结果)19. 已知函数 是定义在 上的奇函数,当 时, .(1)、求函数 在 上的解析式;(2)、用单调性定义证明函数 在区间 上是增函数.20. 已知命题“ ,都有不等式 成立”是真命题.(1)、求实数 的取值集合 ;(2)、设不等式 的解集为 ,若 是 的充分不必要条件,求实数 的取值范围.21. 杭州地铁项目正在如火如荼的进行中,通车后将给市民出行带来便利,已知某条线路通车后,列车的发车时间间隔t(单位:分钟)满足 ,经市场调研测算,列车载客量与发车时间间隔t相关,当 时列车为满载状态,载客量为500人,当 时,载客量会减少,减少的人数与 的平方成正比,且发车时间间隔为2分钟时的载客量为372人,记列车载客量为 .
(1)、求 的值;(2)、画出函数 的图象;(3)、指出函数 的单调区间.(直接写结果)19. 已知函数 是定义在 上的奇函数,当 时, .(1)、求函数 在 上的解析式;(2)、用单调性定义证明函数 在区间 上是增函数.20. 已知命题“ ,都有不等式 成立”是真命题.(1)、求实数 的取值集合 ;(2)、设不等式 的解集为 ,若 是 的充分不必要条件,求实数 的取值范围.21. 杭州地铁项目正在如火如荼的进行中,通车后将给市民出行带来便利,已知某条线路通车后,列车的发车时间间隔t(单位:分钟)满足 ,经市场调研测算,列车载客量与发车时间间隔t相关,当 时列车为满载状态,载客量为500人,当 时,载客量会减少,减少的人数与 的平方成正比,且发车时间间隔为2分钟时的载客量为372人,记列车载客量为 .(Ⅰ)求 的表达式,并求当发车时间间隔为5分钟时,列车的载客量;
(Ⅱ)若该线路每分钟的净收益为 (元),问当发车时间间隔为多少时,该线路每分钟的净收益最大,并求出最大值.
22. 已知幂函数 ,满足 .(1)、求函数 的解析式.(2)、若函数 , ,是否存在实数 使得 的最小值为0?(3)、若函数 ,是否存在实数 ,使函数 在 上的值域为 ?若存在,求出实数 的取值范围;若不存在,说明理由.