四川省广安市岳池县2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期:2021-11-23 类型:期中考试
一、单选题
-
1. 下列四个图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三根木棒首尾依次相接,不能搭成三角形框架的是( )A、 , , B、 , , C、 , , D、 , ,3. 下列四个图形中,线段BE是△ABC的高的是( )A、
2. 下列长度的三根木棒首尾依次相接,不能搭成三角形框架的是( )A、 , , B、 , , C、 , , D、 , ,3. 下列四个图形中,线段BE是△ABC的高的是( )A、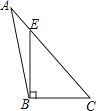 B、
B、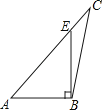 C、
C、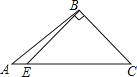 D、
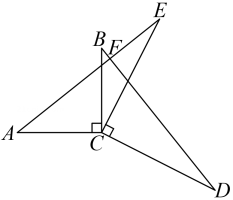
D、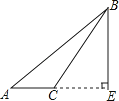 4. 在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为( )A、(-2,3) B、(-2,-3) C、(2,-3) D、(-3,-2)5. 等腰三角形的一边长等于4,一边长等于9,则它的周长是( )A、17 B、22 C、17或22 D、136. 下列说法不正确的是( )A、斜边和一锐角对应相等的两个直角三角形全等; B、有两个角对应相等的两个直角三角形全等; C、等腰三角形的底边上的高线、底边上的中线互相重合; D、点到直线的距离就是该点到该直线的垂线段的长度.7. 如图,已知CD=CA,∠D=∠A,添加下列条件中的( )仍不能证明△ABC≌△DEC.
4. 在平面直角坐标系中,点A(2,3)与点B关于x轴对称,则点B的坐标为( )A、(-2,3) B、(-2,-3) C、(2,-3) D、(-3,-2)5. 等腰三角形的一边长等于4,一边长等于9,则它的周长是( )A、17 B、22 C、17或22 D、136. 下列说法不正确的是( )A、斜边和一锐角对应相等的两个直角三角形全等; B、有两个角对应相等的两个直角三角形全等; C、等腰三角形的底边上的高线、底边上的中线互相重合; D、点到直线的距离就是该点到该直线的垂线段的长度.7. 如图,已知CD=CA,∠D=∠A,添加下列条件中的( )仍不能证明△ABC≌△DEC. A、∠DEC=∠B B、∠ACD=∠BCE C、CE=CB D、DE=AB8. 如图,Rt△ABC中,∠C=90°,斜边AB的垂直平分线交AB于点E,交BC于点D,连接AD,若∠B=35°,则∠CAD的度数为( )
A、∠DEC=∠B B、∠ACD=∠BCE C、CE=CB D、DE=AB8. 如图,Rt△ABC中,∠C=90°,斜边AB的垂直平分线交AB于点E,交BC于点D,连接AD,若∠B=35°,则∠CAD的度数为( )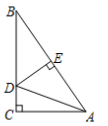 A、20° B、25° C、30° D、35°9. 如图,在 ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=70°,则∠BOC的度数为( )
A、20° B、25° C、30° D、35°9. 如图,在 ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=70°,则∠BOC的度数为( )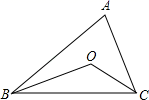 A、125° B、130° C、135° D、140°10. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形, 其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③点O到四条边的距离都相等,④AO=OC.其中正确的结论有( )个.
A、125° B、130° C、135° D、140°10. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形, 其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③点O到四条边的距离都相等,④AO=OC.其中正确的结论有( )个. A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 如图,工人师傅砌门常用木条EF固定长方形门框ABCD,这种方法应用的数学知识是三角形的.
 12. 等腰三角形一个顶角等于70 ,则它的底角为.13. 一个多边形的内角和比四边形内角和的4倍多180°,这个多边形的边数是.14. 如图,要测量河两岸相对两点A、B间的距离,在河岸BM上截取BC=CD,作DE⊥BD交AC的延长线于点E,垂足为点D,测得ED=3,CD=4,则A、B两点间的距离等于.
12. 等腰三角形一个顶角等于70 ,则它的底角为.13. 一个多边形的内角和比四边形内角和的4倍多180°,这个多边形的边数是.14. 如图,要测量河两岸相对两点A、B间的距离,在河岸BM上截取BC=CD,作DE⊥BD交AC的延长线于点E,垂足为点D,测得ED=3,CD=4,则A、B两点间的距离等于. 15. 如图,在△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点M,交AB于点N.连接MB,若AB=8,△MBC的周长是14,则BC的长为.
15. 如图,在△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点M,交AB于点N.连接MB,若AB=8,△MBC的周长是14,则BC的长为. 16. 如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=.
16. 如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=.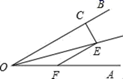
三、解答题
-
17. 已知,如图,在△ABC中,AD、AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.求∠BAC和∠DAE的度数.
 18. 如图,点 , 在 上, , , ,求证: .
18. 如图,点 , 在 上, , , ,求证: .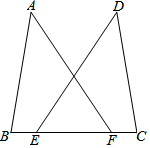 19. 已知:如图,AD=BC,AC=BD.试证明:∠CAD=∠DBC.
19. 已知:如图,AD=BC,AC=BD.试证明:∠CAD=∠DBC.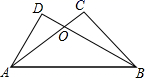 20. 如图,方格纸中每个小方格都是边长为1的正方形,四边形ABCD的顶点与点E都是格点.
20. 如图,方格纸中每个小方格都是边长为1的正方形,四边形ABCD的顶点与点E都是格点. (1)、作出四边形ABCD关于直线AC对称的四边形AB′CD′;(2)、求四边形ABCD的面积;(3)、若在直线AC上有一点P,使得P到D、E的距离之和最小,请作出点P的位置.21. 货轮在海上以每小时6海里的速度沿南偏东40°的方向航行,已知货轮在B处时,测得灯塔A在其北偏东80°的方向上,航行半小时后货轮到达C处,此时测得灯塔A在其北偏东20°的方向上,求货轮到达C处时与灯塔A的距离.
(1)、作出四边形ABCD关于直线AC对称的四边形AB′CD′;(2)、求四边形ABCD的面积;(3)、若在直线AC上有一点P,使得P到D、E的距离之和最小,请作出点P的位置.21. 货轮在海上以每小时6海里的速度沿南偏东40°的方向航行,已知货轮在B处时,测得灯塔A在其北偏东80°的方向上,航行半小时后货轮到达C处,此时测得灯塔A在其北偏东20°的方向上,求货轮到达C处时与灯塔A的距离.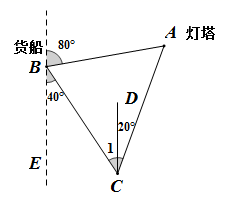 22. 王强同学用10块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板 ,点C在 上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.
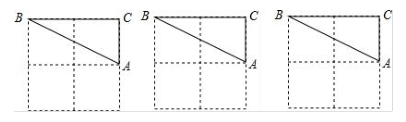
22. 王强同学用10块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板 ,点C在 上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离. 23. 如图,在2×2的正方形网格中,每个小正方形的边长均为1.请分别在下列图中画一个位置不同、顶点都在格点上的三角形,使其与 成轴对称图形.
23. 如图,在2×2的正方形网格中,每个小正方形的边长均为1.请分别在下列图中画一个位置不同、顶点都在格点上的三角形,使其与 成轴对称图形.