江苏省无锡市江阴市2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期:2021-11-23 类型:期中考试
一、单选题
-
1. 改革开放以来,我国众多科技实体在各自行业取得了举世瞩目的成就,大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表.上述四个企业的标志是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组数中不能作为直角三角形的三边长的是( )A、6,12,8 B、7,24,25 C、1.5,2,2.5 D、9,12,153. 等腰三角形的顶角等于80°,则它的底角是( )A、80° B、50° C、40° D、80°或50°4. 下列说法不正确的是( )A、等腰三角形的对称轴是底边的垂直平分线 B、等腰直角三角形底边上的高线等于底边的一半 C、直角三角形中有一个角是30°,则这个角所对的直角边是斜边的一半 D、等边三角形有一条对称轴5. 如图,在△ABC中,AB=AC,AC的垂直平分线l交BC于点D.若∠BAD=78°,则∠B的度数是( )
2. 下列各组数中不能作为直角三角形的三边长的是( )A、6,12,8 B、7,24,25 C、1.5,2,2.5 D、9,12,153. 等腰三角形的顶角等于80°,则它的底角是( )A、80° B、50° C、40° D、80°或50°4. 下列说法不正确的是( )A、等腰三角形的对称轴是底边的垂直平分线 B、等腰直角三角形底边上的高线等于底边的一半 C、直角三角形中有一个角是30°,则这个角所对的直角边是斜边的一半 D、等边三角形有一条对称轴5. 如图,在△ABC中,AB=AC,AC的垂直平分线l交BC于点D.若∠BAD=78°,则∠B的度数是( )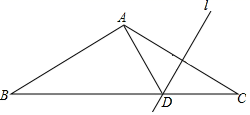 A、34° B、30° C、28° D、26°6. 如图,在△ABC中,AB=AC,∠BAC=46°,∠BAC的平分线与AB的垂直平分线OD交于点O,点E在BC上,点F在AC上,连接EF.将∠C沿EF折叠,点C与点O恰好重合时,则∠OEC的度数( )
A、34° B、30° C、28° D、26°6. 如图,在△ABC中,AB=AC,∠BAC=46°,∠BAC的平分线与AB的垂直平分线OD交于点O,点E在BC上,点F在AC上,连接EF.将∠C沿EF折叠,点C与点O恰好重合时,则∠OEC的度数( ) A、90° B、92° C、95° D、98°7. 有一个边长为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了如图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是( )
A、90° B、92° C、95° D、98°7. 有一个边长为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了如图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是( ) A、2022 B、2021 C、2020 D、18. 如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )
A、2022 B、2021 C、2020 D、18. 如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( ) A、 cm B、11cm C、13cm D、17cm9. 如图,在 ABC中,∠ACB=90°,∠A=30°,AB=8,点P是AC上的动点,连接BP,以BP为边作等边 BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是( )
A、 cm B、11cm C、13cm D、17cm9. 如图,在 ABC中,∠ACB=90°,∠A=30°,AB=8,点P是AC上的动点,连接BP,以BP为边作等边 BPQ,连接CQ,则点P在运动过程中,线段CQ长度的最小值是( ) A、2 B、4 C、 D、10. 如图, ,点B和点C是对应顶点, ,记 ,当 时, 与 之间的数量关系为( )
A、2 B、4 C、 D、10. 如图, ,点B和点C是对应顶点, ,记 ,当 时, 与 之间的数量关系为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知等腰三角形的两边长为3和6,则它的周长为.12. 已知:如图,在 中,点 在边 上, ,则 度.
 13. 如图,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有种.
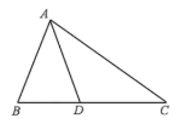
13. 如图,正三角形网格中,已有两个小正三角形被涂黑,再将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有种. 14. 一个三角形的三边为6、10、x,另一个三角形的三边为 、6、12,如果这两个三角形全等,则 =.15. 如图,在△ABC中,点D在边BC上,AB=AD,点E,点F分别是AC,BD的中点,EF=3,则AC的长为.
14. 一个三角形的三边为6、10、x,另一个三角形的三边为 、6、12,如果这两个三角形全等,则 =.15. 如图,在△ABC中,点D在边BC上,AB=AD,点E,点F分别是AC,BD的中点,EF=3,则AC的长为. 16. 如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8.若S△ABC=21,则DE=.
16. 如图,BD平分∠ABC,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8.若S△ABC=21,则DE=. 17. 在Rt△ABC中,∠ABC=90°,AB=3,BC=4,点E,F分别在边AB,AC上,将△AEF沿直线EF翻折,点A落在点P处,且点P在直线BC上.则线段CP长的取值范围是.
17. 在Rt△ABC中,∠ABC=90°,AB=3,BC=4,点E,F分别在边AB,AC上,将△AEF沿直线EF翻折,点A落在点P处,且点P在直线BC上.则线段CP长的取值范围是.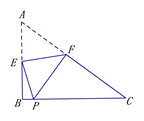
三、解答题
-
18. 如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).

( 1 )在图中作出△ABC关于直线l对称的△A1B1C1;(要求:A与A1 , B与B1 , C与C1相对应)
( 2 )若有一格点P到点A、B的距离相等(PA=PB),则网格中满足条件的点P共有 ▲ 个;
( 3 )在直线l上找一点Q,使QB+QC的值最小.
19. 若正数x的两个平方根为2m-3和4m-5,求x的值.20. 如图,已知AB=DC,AC=DB.求证:∠1=∠2.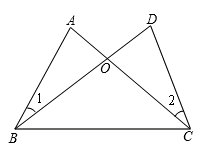 21. 如图,在2×2的正方形网格中,每个小正方形的边长均为1.请分别在下列图中画一个位置不同、顶点都在格点上的三角形,使其与 成轴对称图形.
21. 如图,在2×2的正方形网格中,每个小正方形的边长均为1.请分别在下列图中画一个位置不同、顶点都在格点上的三角形,使其与 成轴对称图形.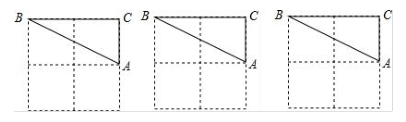 22. 如图,OA⊥OB,OA=45海里,OB=15海里,有一海岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向海岛O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
22. 如图,OA⊥OB,OA=45海里,OB=15海里,有一海岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向海岛O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船. (1)、请用直尺和圆规作出C处的位置;(2)、求我国海监船行驶的航程BC的长.23. 如图,在△ABC中,AD是高,CE是中线,DG垂直平分CE,连接DE.
(1)、请用直尺和圆规作出C处的位置;(2)、求我国海监船行驶的航程BC的长.23. 如图,在△ABC中,AD是高,CE是中线,DG垂直平分CE,连接DE.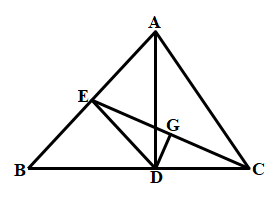 (1)、求证:DC=BE;(2)、若∠AEC=72°,求∠BCE的度数.24. 如图1,在△ABC中,AB=AC,G为三角形外一点,且△GBC为等边三角形.
(1)、求证:DC=BE;(2)、若∠AEC=72°,求∠BCE的度数.24. 如图1,在△ABC中,AB=AC,G为三角形外一点,且△GBC为等边三角形.
 (1)、求证:直线AG垂直平分BC;(2)、以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说明理由.25. 如图,在四边形ABCD中,∠ABC=∠BCD=90°,AB=BC=5cm,CD=4cm.点P从点C出发以1cm/s的速度沿CB向点B匀速移动,点M从点A出发以1.5cm/s的速度沿AB向点B匀速移动,点N从点D出发以acm/s的速度沿DC向点C匀速移动.点P、M、N同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为ts.
(1)、求证:直线AG垂直平分BC;(2)、以AB为一边作等边△ABE(如图2),连接EG、EC,试判断△EGC是否构成直角三角形?请说明理由.25. 如图,在四边形ABCD中,∠ABC=∠BCD=90°,AB=BC=5cm,CD=4cm.点P从点C出发以1cm/s的速度沿CB向点B匀速移动,点M从点A出发以1.5cm/s的速度沿AB向点B匀速移动,点N从点D出发以acm/s的速度沿DC向点C匀速移动.点P、M、N同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为ts. (1)、如图1,①当a为何值时,以P、B、M为顶点的三角形与△PCN全等?并求出相应的t的值; ②连接AP、BD交于点E.当AP⊥BD时,求出t的值;(2)、如图2,连接AN、MD交于点F.当 , 时,证明S△ADF=S△CDF.
(1)、如图1,①当a为何值时,以P、B、M为顶点的三角形与△PCN全等?并求出相应的t的值; ②连接AP、BD交于点E.当AP⊥BD时,求出t的值;(2)、如图2,连接AN、MD交于点F.当 , 时,证明S△ADF=S△CDF.