江苏省连云港市灌云县2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期:2021-11-23 类型:期中考试
一、单选题
-
1. 将一张长方形纸对折,然后用笔尖在纸上扎出“B”,再把纸铺平,可以看到的是( )A、
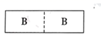 B、
B、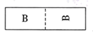 C、
C、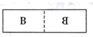 D、
D、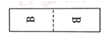 2. 下列各组数中,哪一组是勾股数( )A、 , , B、6,7,8 C、3,4,6 D、9,40,413. 一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
2. 下列各组数中,哪一组是勾股数( )A、 , , B、6,7,8 C、3,4,6 D、9,40,413. 一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )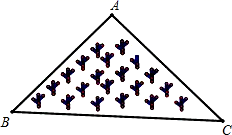 A、 ABC 的三条中线的交点 B、 ABC 三边的垂直平分线线的交点 C、 ABC 三条角平分线的交点 D、 ABC 三条高所在直线的交点4. 如图,在一块平地上,张大爷家屋前9米远处有一棵大树,在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米,大树倒下时能砸到张大爷的房子吗( )
A、 ABC 的三条中线的交点 B、 ABC 三边的垂直平分线线的交点 C、 ABC 三条角平分线的交点 D、 ABC 三条高所在直线的交点4. 如图,在一块平地上,张大爷家屋前9米远处有一棵大树,在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米,大树倒下时能砸到张大爷的房子吗( )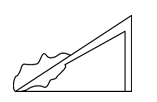 A、一定不会 B、可能会 C、一定会 D、以上答案都不对5. 如图, , ,要使得 ,需要补充的条件不能是( )
A、一定不会 B、可能会 C、一定会 D、以上答案都不对5. 如图, , ,要使得 ,需要补充的条件不能是( )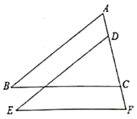 A、 B、 C、 D、6. 如图,在△ABC中,已知∠B和∠C的平分线相交于点D,过点D作EF∥BC交AB、AC于点E、F,若△AEF的周长为9,BC=6,则△ABC的周长为( )
A、 B、 C、 D、6. 如图,在△ABC中,已知∠B和∠C的平分线相交于点D,过点D作EF∥BC交AB、AC于点E、F,若△AEF的周长为9,BC=6,则△ABC的周长为( )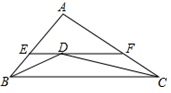 A、18 B、17 C、16 D、157. 如图,Rt△ABC中,∠C=90°,∠A<∠B , 且∠A≠30°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点P在△ABC的其他边上,则可以画出不同的点P的个数为( )
A、18 B、17 C、16 D、157. 如图,Rt△ABC中,∠C=90°,∠A<∠B , 且∠A≠30°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点P在△ABC的其他边上,则可以画出不同的点P的个数为( )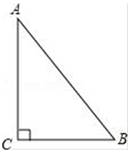 A、4 B、5 C、6 D、78. 如图,已知 和 都是等边三角形,且A、C、E三点共线. 与 交于点O, 与 交于点P, 与 交于点Q,连结 .以下六个结论:① ;② ;③ ;④ ;⑤ ;⑥ .其中正确结论的有( )个
A、4 B、5 C、6 D、78. 如图,已知 和 都是等边三角形,且A、C、E三点共线. 与 交于点O, 与 交于点P, 与 交于点Q,连结 .以下六个结论:① ;② ;③ ;④ ;⑤ ;⑥ .其中正确结论的有( )个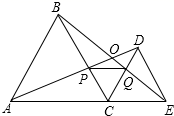 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
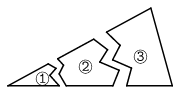
9. 如图所示,某同学将一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带第块去.(填序号)
 10. 如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得 , ,则M,C两点间的距离为km.
10. 如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开,若测得 , ,则M,C两点间的距离为km.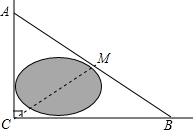 11. 如果等腰三角形的两边长分别为3和2,则它的周长为.12. 如图,把一张长方形纸片 沿 折叠,点D与点C分别落在点 和点 的位置上, 与 的交点为G,若 ,则 为度.
11. 如果等腰三角形的两边长分别为3和2,则它的周长为.12. 如图,把一张长方形纸片 沿 折叠,点D与点C分别落在点 和点 的位置上, 与 的交点为G,若 ,则 为度.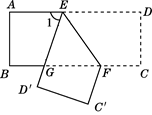 13. 如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则BD2=.
13. 如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则BD2=. 14. 如图,在等腰 中, ,点D、E、F分别是边AB、BC、CA上的点,DE与BF相交于点G, , ,若 ,则 的度数为.
14. 如图,在等腰 中, ,点D、E、F分别是边AB、BC、CA上的点,DE与BF相交于点G, , ,若 ,则 的度数为.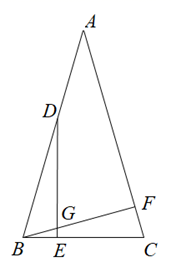 15. 如图,在 中, 、 的垂直平分线分别交 于D、E两点,并且相交于点F,且 ,则 的度数是.
15. 如图,在 中, 、 的垂直平分线分别交 于D、E两点,并且相交于点F,且 ,则 的度数是.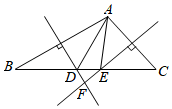 16. 如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连BM、BN,当BM+BN最小时,∠MBN=度.
16. 如图,等边△ABC中,AD为BC边上的高,点M、N分别在AD、AC上,且AM=CN,连BM、BN,当BM+BN最小时,∠MBN=度.
三、解答题
-
17. 已知:如图,AB、CD相交于点E,且E是AB、CD的中点.求证: .
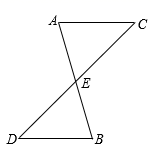 18. 已知:如图,在 中,D是BC的中点,点E、F分别在AB、AC上,且 , .求证: , .
18. 已知:如图,在 中,D是BC的中点,点E、F分别在AB、AC上,且 , .求证: , .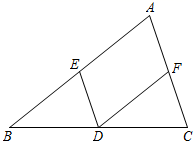 19. 如图,在四边形ABCD中,AC、BD相交于点O,AB=DC,∠1=∠2.求证:AC=BD.
19. 如图,在四边形ABCD中,AC、BD相交于点O,AB=DC,∠1=∠2.求证:AC=BD.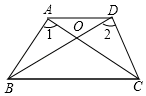 20. 已知,如图,AD=BC,CA⊥AB,AC⊥CD.求证:AD∥BC.
20. 已知,如图,AD=BC,CA⊥AB,AC⊥CD.求证:AD∥BC.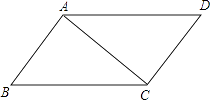 21. 已知:如图,AD、BF相交于点O,AB=DF.点E、C在BF上,且BE=FC,AC=DE.求证:OA=OD,OB=OF.
21. 已知:如图,AD、BF相交于点O,AB=DF.点E、C在BF上,且BE=FC,AC=DE.求证:OA=OD,OB=OF.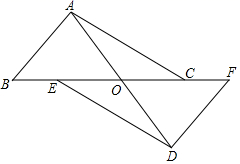 22. 已知:如图∠BAC的角平分线与BC的垂直平分线交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.
22. 已知:如图∠BAC的角平分线与BC的垂直平分线交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.求证:BE=CF.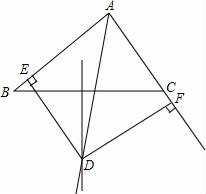 23. 已知:如图,在 中, , ,D是AB的中点,点E在AC上,点F在BC上,且 .求证: .
23. 已知:如图,在 中, , ,D是AB的中点,点E在AC上,点F在BC上,且 .求证: .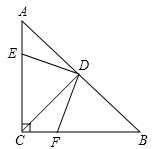 24. 某小区有一块如图所示的四边形空地ABCD,为了庆祝建党百年,小区物业决定在这块空地上种植花草,测得已知 , , , , .种植花草的费用为80元 ,则该空地种植花草共需多少元?
24. 某小区有一块如图所示的四边形空地ABCD,为了庆祝建党百年,小区物业决定在这块空地上种植花草,测得已知 , , , , .种植花草的费用为80元 ,则该空地种植花草共需多少元?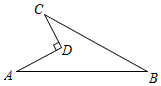 25. 如图1,△ABC是等腰直角三角形,∠ACB=90°,AC=BC.D是BC上任意一点(点D与点B,C都不重合),连接AD,CF⊥AD,交AD于点E,交AB于点F,BG⊥BC交CF的延长线于点G.
25. 如图1,△ABC是等腰直角三角形,∠ACB=90°,AC=BC.D是BC上任意一点(点D与点B,C都不重合),连接AD,CF⊥AD,交AD于点E,交AB于点F,BG⊥BC交CF的延长线于点G.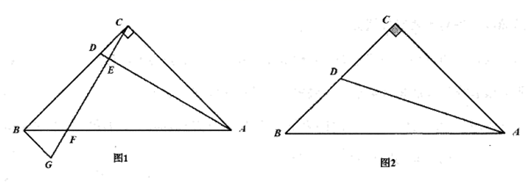 (1)、写出与BG相等的线段,并证明;(2)、若点D为线段BC的中点,其余条件不变,连接DF.根据题意,先在图2中补全图形,再证明:∠BDF=∠CDE.26. (教材呈现)如图,在 中,D是边BC的中点,过点C画直线CE,使 ,交AD的延长线于点E,求证:
(1)、写出与BG相等的线段,并证明;(2)、若点D为线段BC的中点,其余条件不变,连接DF.根据题意,先在图2中补全图形,再证明:∠BDF=∠CDE.26. (教材呈现)如图,在 中,D是边BC的中点,过点C画直线CE,使 ,交AD的延长线于点E,求证: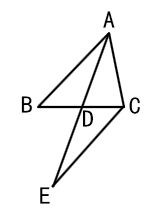
证明∵ (已知)
∴ , (两直线平行,内错角相等).
在 与 中,
∵ , (已证),
(已知),
∴ ,
∴ (全等三角形的对应边相等).
(1)、(方法应用)如图①,在 中, , ,则BC边上的中线AD长度的取值范围是.
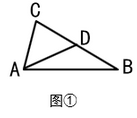 (2)、(猜想证明)如图②,在四边形ABCD中, ,点E是BC的中点,若AE是 的平分线,试猜想线段AB、AD、DC之间的数量关系,并证明你的猜想;
(2)、(猜想证明)如图②,在四边形ABCD中, ,点E是BC的中点,若AE是 的平分线,试猜想线段AB、AD、DC之间的数量关系,并证明你的猜想;
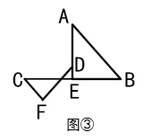
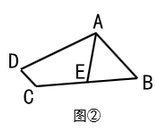 (3)、(拓展延伸)如图③,已知 ,点E是BC的中点,点D在线段AE上, ,若 , ,求出线段DF的长.
(3)、(拓展延伸)如图③,已知 ,点E是BC的中点,点D在线段AE上, ,若 , ,求出线段DF的长.