江苏省江阴市澄要片2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期：2021-11-23 类型：期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 4的平方根是（ ）A、±2 B、﹣2 C、2 D、3. 等腰三角形有两条边的长分别为3和4，则该三角形的周长为（ ）A、10 B、10或11 C、11 D、7或114. 到三角形的三个顶点距离相等的点是（ ）.A、三角形三条中线的交点 B、三角形三边垂直平分线的交点 C、三角形三条角平分线的交点 D、三角形三条高的交点5. 下列四组线段中，可以构成直角三角形的是（ ）A、4cm、5cm、6cm B、1cm、1.5cm、3cm C、2cm、3cm、4cm D、1.5cm、2cm、2.5cm6. “三角形具有稳定性”这个事实说明了（ ）A、SAS B、ASA C、AAS D、SSS7. 如图，△ABC和△DEF中，AB=DE、角∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF（ ）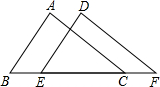
A、AC∥DF B、∠A=∠D C、AC=DF D、∠ACB=∠F8. 如图，AD平分∠BAC交BC于点D，DE⊥AB于点E，DF⊥AC于点F.若S△ABC=12，DF=2，AC=3，则AB的长是（ ）
A、9 B、7 C、4 D、29. 如图，△ABC中，AB=AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则∠EFC的度数为（ ）
A、35° B、40° C、45° D、60°10. 如图，△ABC中，BC＝4，D、E 分别是线段AB和线段BC上的动点，且BD=DE，F是线段AC上一点，且EF=FC，则DF的最小值为（ ）
A、3 B、2 C、2.5 D、4二、填空题
-
11. 一个汽车牌照在水中的倒影为
，则该汽车牌照号码为.
12. 如果等腰三角形有一个内角为110°，则其底角的度数是.13. 在△ABC 中， ∠C= 90° ，AC=3，BC=4，D 是 AB 边的中点，则 CD=.14. 已知△ACB≌△A′C B′，∠B=70°，则∠B′的度数为.15. 一个正数的两个平方根分别是2a＋5和2a－1，则这个正数为.16. 如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”.他们仅仅少走了步路(假设2步为1米)，却踩伤了花草.
17. 如图，△ABC中，AC－AB＝4，AD是∠BAC的角平分线，CD⊥AD，若△BCD的面积最大值为20，此时BC=.
18. 如图，有一个直角三角形ABC，∠C=90°，AC=8，BC=3，P、Q两点分别在边AC和过点A且垂直于AC的射线AX上运动，且PQ=AB.问当AP=时，才能使△ABC和△PQA全等.
三、解答题
-
19. 已知：如图，AC、DB相交于点O，AB＝DC，∠ABO＝∠DCO.
求证：
(1)、△ABO≌△DCO；(2)、若∠OBC＝35°，求∠OCB的度数.20. 如图，在正方形网格中，点A、B、C、M、N都在格点上.
(1)、作△ABC关于直线MN对称的图形△A'B'C'；(2)、作出AB边上的中线；(3)、若每个小正方形边长均为1，则△ABC的面积=.21. 如图，在Rt△ABC中，∠C=90°，AC=12，BC=9.
(1)、请用无刻度的直尺和圆规在AC上找一点E，使得AE=BE；(2)、求CE的长.22. 如图所示，长方形纸片ABCD的长AD＝8cm，宽AB＝4cm，将其沿着折痕EF折叠，使点D与点B重合.
(1)、求证：BE＝BF；(2)、求折叠后△BEF的面积.23. 如图，△ABC中，∠ACB＝90°，点D是边BC上一点，DE⊥AB于点E，点F是线段AD的中点，连接EF，CF.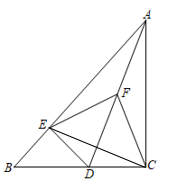
(1)、求证：EF＝CF；(2)、若∠BAC=30°，连接EC，试判断△EFC 的形状，并说明理由.24. 如图，在四边形 中， 将 绕点C顺时针旋转一定角度后，点B的对应点恰好与点A重合，得到 .
(1)、求证： ；(2)、若 ，试求四边形 的对角线 的长.25. 如图1，已知长方形ABCD，AB＝CD＝2，BC＝AD＝3，∠A＝∠B＝∠C＝∠D＝90°，E为CD边的中点，P为长方形ABCD边上的动点，动点P从A出发，沿着A→B→C→E运动到E点停止，设点P 经过的路程为x，△APE的面积为y.
(1)、当x=1时，y=；当x=5.5时，y=；(2)、如图2，求出当点P边BC时，用x的代数式表示y；(3)、如备用图，当P在线段BC上运动时，是否存在点P使得△APE的周长最小？若存在，求出此时∠PAD的度数；若不存在，请说明理由.26. 问题背景：(1)、如图1；在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°.E，F分别是BC，CD上的点，且∠EAF＝60°.探究图中线段BE，EF，FD之间的数量关系.小王同学探究此问题的方法是，延长FD到点G，使DG＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；
(2)、如图2：已知四边形ABCD是边长为1的正方形，点E是线段BC上的动点，以AE为直角边在直线BC的上方作等腰直角三角形AEF，∠AEF＝90°.①求证：QE=BE+DQ；
②过P作PH⊥EQ，垂足为H，求证：PC=PH.