湖南省长沙市明德集团2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期：2021-11-23 类型：期中考试
一、单选题
-
1. 在下面由冬季奥运会比赛项目图标组成的四个图形中，其中可以看作轴对称图形的是（ ）A、
B、
C、
D、
2. 下列长度的3根小木棒不能搭成三角形的是（ ）A、2cm，3cm，4cm B、1cm，2cm，3cm C、3cm，4cm，5cm D、4cm，5cm，6cm3. 如图，△ABC≌△DEC，∠A＝70°，∠ACB＝60°，则∠E的度数为（ ）
A、70° B、50° C、60° D、30°4. 下列命题是假命题的是（ ）A、三角形的三条中线都在三角形的内部 B、等腰三角形底边的中点到两腰的距离相等 C、有一个角是60°的等腰三角形是等边三角形 D、全等的两个三角形一定关于某直线成轴对称5.如图，AB∥CD，点E在BC上，且CD=CE，∠D=74°，则∠B的度数为（ ）
A、74° B、32° C、22° D、16°6. 在平面直角坐标系中，点P（1，-2）关于y轴的对称点的坐标是（ ）A、(-1，-2) B、(-1，2) C、(1，2) D、(2，-1)7. 如图，若MB＝ND，∠MBA＝∠NDC，下列条件中不能判定 的是（ ）
A、AM＝CN B、 C、AB＝CD D、∠M＝∠N8. 如图，在测量一个小口圆形容器的壁厚时，李师傅用“X型转动钳”按如图方法进行测量，其中O是AD、CB的中点，由三角形全等的知识可知只要测量A、B的距离，即得C、D的距离，便能计算出圆形容器的壁厚.请问李师傅得到△AOB≌△COD的依据是（ ）
A、SAS B、SSS C、ASA D、HL9. 如图，等腰三角形ABC的周长为21，底边BC的长为5，腰AB的垂直平分线交AB于点D，交AC于点E，连接BE，则△BEC的周长为( )
A、11 B、12 C、13 D、1410. 如图，在学习了轴对称后，小华在课外研究三角板时发现“两块完全相同的含有30°的三角板可以拼成一个等边三角形”，请你帮他解决以下问题：在直角△ABC中，∠ACB＝90°，∠A＝30°，AC＝6，BC＝ ，点E，P分别在斜边AB和直角边AC上，则EP＋BP的最小值是（ ）
A、 B、4 C、6 D、二、填空题
-
11. 某个正多边形有一个外角是36°，则这个正多边形是 边形.12. 如图，D、E分别为AB、AC边上的点，∠B＝∠C，BE＝CD.若AB＝7，CE＝4，则AD的长度为.
13. 将一张长方形纸片按如图所示的方式折叠， 、 为折痕，若 ，则 为度.
14. 如图，小明与小红玩跷跷板游戏，如果跷跷板的支点O（即跷跷板的中点）至地面的距离是50cm，当小红从水平位置CD下降30cm时，这时小明离地面的高度是cm.
15. 如图，在 中， ，点E在 的延长线上， 于点P，交 于点F，若 ，则 的长度为.
16. 如图，在△OAB和△OCD中，OA＝OB，OC＝OD，OA＞OC，∠AOB＝∠COD＝40°，连接AC，BD交于点M，连接OM.下列结论：①AC＝BD；②∠AMB＝40°；③OM平分∠BOC；④MO平分∠BMC.其中正确的是
三、解答题
-
17. 已知一个多边形的内角和比外角和多540°，请求出它是几边形？18. 如图，AD是△ABC的BC边上的高，AE平分∠BAC，若∠B＝40°，∠C＝80°，求∠BAE和∠DAE的度数.
19. 如图，已知A（﹣1，5），B（﹣1，1），C（﹣4，3）.
(1)、作出△ABC关于x轴对称的图形△A′B′C′；(2)、求△ABC的面积.20. 如图，在△ABC中，分别以点A，B为圆心，以大于 AB的长为半径画弧，两弧相交于点M和N，作直线MN，交AC于点E，连接BE，
(1)、请根据作图过程回答问题：直线MN是线段AB的（ ）.A、角平分线 B、垂直平分线 C、高 D、中线(2)、若 中， ， ， ，求AC的长.21. 如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC＝CD.
(1)、求证：△BCE≌△DCF；(2)、若BE＝2，AD＝5，求线段AF的长.22. 如图，△ 是等边三角形， 是AC边上的高，延长 至E，使 .
(1)、求证： ；(2)、过点D作 垂直 ，垂足为F，若 ，求△ 的周长.23. 如图，在△ 中，AD⊥BC，垂足为D，AD＝CD，点E在AD上，DE＝BD＝2，M、N分别是AB、CE的中点.
(1)、求证：△ADB≌△CDE；(2)、求∠MDN的度数.(3)、若CD＝5，求△AMD的面积.24. 新定义：在△ABC中，若存在一个内角是另外一个内角度数的n倍（n为大于1的正整数），则称△ABC为n倍角三角形.例如，在△ABC中，∠A＝80°，∠B＝60°，∠C＝40°，可知∠A＝2∠C，所以△ABC为2倍角三角形.
(1)、在△DEF中，∠E＝40°，∠F＝35°，则△DEF为倍角三角形.(2)、如图1，直线MN与直线PQ相交于O，∠POM＝30°，点A、点B分别是射线OP、OM上的动点；已知∠BAO、∠OBA的角平分线交于点C，在△ABC中，如果有一个角是另一个角的2倍，请求出∠BAC的度数.(3)、如图2，直线MN⊥直线PQ于点O，点A、点B分别在射线OP、OM上；已知∠BAO、∠OAG的角平分线分别与∠BOQ的角平分线所在的直线交于点E、F；若△AEF为3倍角三角形，试求∠ABO的度数.25. 在平面直角坐标系中，点A的坐标为 ，点B为y轴正半轴上的一个动点，以B为直角顶点，AB为直角边在第一象限作等腰 .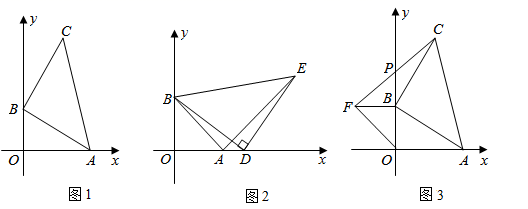
(1)、如图1，若OB＝6，则点C的坐标为；(2)、如图2，若OB＝8，点D为OA延长线上一点，以D为直角顶点，BD为直角边在第一象限作等腰 ，连接AE，求证：AE⊥AB；(3)、如图3，以B为直角顶点，OB为直角边在第三象限作等腰 .连接CF，交y轴于点P，求线段BP的长.