湖北省武汉市江汉区2021-2022学年八年级上学期数学期中考试试卷

试卷更新日期：2021-11-23 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 下列三个图形中，具有稳定性的图形个数是（   ）

    A、0个 B、1个 C、2个 D、3个

    查看试题解析

  • 2. 下列计算正确的是（   ）
    A、（3a）3＝9a3 B、a3＋a2＝a6 C、a·a2＝a2 D、（a3）2＝a6

    查看试题解析

  • 3. 下面作三角形最长边上的高正确的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 4. 已知图中的两个三角形全等，则∠α的度数是（   ）

    A、72° B、60° C、58° D、50°

    查看试题解析

  • 5. 下列添括号正确的是（   ）
    A、a＋b－c＝a－（b－c） B、a＋b－c＝a＋（b－c） C、a－b－c＝a－（b－c） D、a－b＋c＝a＋（b－c）

    查看试题解析

  • 6. 下列条件不能判定两个直角三角形全等的是（   ）
    A、两条直角边对应相等 B、斜边和一锐角对应相等 C、斜边和一直角边对应相等 D、两个直角三角形的面积相等

    查看试题解析

  • 7. 若 am=128 ， an=8 ，则 am−n 值是（   ）
    A、120 B、－120 C、16 D、116

    查看试题解析

  • 8. 如图，在 △ABC 中，D，E分别是边 AC ， BC 上的点，若 △ADB≌△EDB≌△EDC ，则 ∠C 的度数为（   ）

    A、15° B、20° C、25° D、30°

    查看试题解析

  • 9. 如图，在 △ ABC和 △ BDE中，点C在边BD上，边AC交边BE于点F.若AC＝BD，AB＝ED，BC＝BE，则∠ACB等于（   ）

    A、∠EDB B、∠BED C、12 ∠AFB D、2∠ABF

    查看试题解析

  • 10. 如图，在△ABC中，AB＝8cm，BC＝6cm，AC＝5cm.沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，则△AED 的周长是（   ）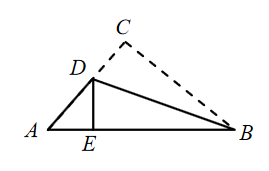

    A、5cm B、6cm C、7cm D、8cm

    查看试题解析

二、填空题

  • 11. 计算（－2）2×（－2）3＝.

    查看试题解析

  • 12. 如图，AC和BD相交于O点，若OA＝OD，用“AAS”证明△AOB≌△DOC还需增加条件.

    查看试题解析

  • 13. 如图， △ACE≌△BDF .若AD＝8，BC＝3，则AB的长是.

    查看试题解析

  • 14. 如图，在 △ ABC和 △ DEC中，AB＝DE，AC＝DC，CE＝CB.点E在AB上，若∠ACE＝2∠ECB＝50°，则∠D＝.

    查看试题解析

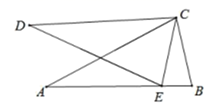  • 15. 一个正方形的边长增加2cm，它的面积就增加24cm，这个正方形的边长是cm．

    查看试题解析

  • 16. 已知（x－p）2＝x2＋mx＋36，则m＝.

    查看试题解析

  • 17. 如图，在△ABC中，AD⊥BC， CE⊥AB，垂足分别是D，E.AD，CE交于点H，已知AE＝CE＝5，CH＝2，则BE＝.

    查看试题解析

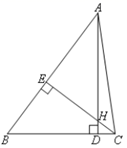  • 18. 如图是今年某月的日历表（隐去日期），表中a，b，c，d表示该方框中日期的数值，则bc－ad＝.

    查看试题解析

  • 19. 一个n边形，若其中(n－1)个内角的和为800°，则n＝.

    查看试题解析

  • 20. 如图，正方形的边长为m＋5，面积记为S1 ， 长方形的两边长分别为m＋3，m＋9，面积记为S2（其中m为正整数）.若某个图形的面积S介于S1 ， S2之间（不包括S1 ， S2），S的整数值有且只有15个，则m＝.

    查看试题解析

三、解答题

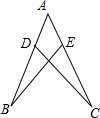
  • 21. 计算：
    (1)、7m（4m2p）2÷7m2；             
    (2)、（15x2y－10xy2）÷5xy.

    查看试题解析

  • 22. 如图，AB＝AC，点D、E分别在AB、AC上，AD＝AE，求证：CD＝BE.

    查看试题解析

  • 23. 计算：
    (1)、x2（x－1）－（x＋1）（x2＋x）；
    (2)、（2x＋1）2－（x＋3）（x－3）－（x－1）2

    查看试题解析

  • 24. 如图，已知△ABC三个顶点的坐标分别为A（2，3），B（4，0），C（1，0）.

    (1)、画△ABC，直接写出△ABC的面积；
    (2)、画格点D，连接AD，使直线AD平分△ABC的面积；
    (3)、若∠CAE＝45°，直接写出满足条件的格点E的个数.

    查看试题解析

  • 25. 如图，在 △ABC 中， AD 是角平分线， DE⊥AB 于点 E ， F 在边AC上， BD=DF .

    (1)、如图1，若 ∠C=90° ，求证： △FCD≌△BED ；
    (2)、如图2，求证： AB−AF=2EB ；
    (3)、若 AC=8 ， AB=10 ， BC=6 ，直接写出 DF 的长.

    查看试题解析

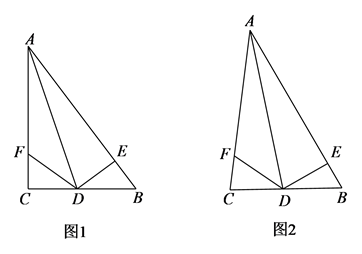  • 26.
    (1)、已知2x2＋6x＝3，求代数式x（x＋1）（x＋2）（x＋3）的值；
    (2)、如果多项式4x2＋kx－7被4x＋3除后余2，求k的值.

    查看试题解析

  • 27. 如图，四边形ABCD中，AB∥CD，∠C＝110°.E为BC的中点，直线FG经过点E，DG⊥FG于点G，BF⊥FG于点F.

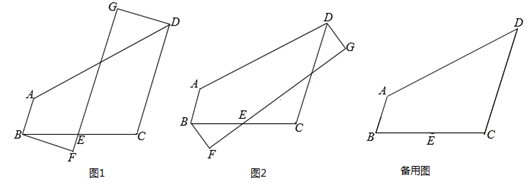    (1)、如图1，当∠BEF＝70°时，求证：DG＝BF；
    (2)、如图2，当∠BEF≠70°时，若BC＝DC，DG＝BF，请直接写出∠BEF的度数；
    (3)、当DG－BF的值最大时，直接写出∠BEF的度数.

    查看试题解析

  • 28. 在平面直角坐标系中，已知点A（0，a），B（b，0），其中a，b满足：（x＋b）（x＋2）＝x2＋ax＋6（a，b为常数）.

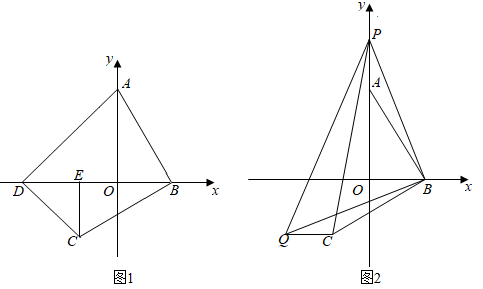    (1)、求点A，B的坐标；
    (2)、如图1，D为x轴负半轴上一点，C为第三象限内一点，且∠ABC＝∠ADC＝90°，AO＝DO，DB平分∠ADC.过点C作CE⊥DB于点E，求证：DE＝OB；
    (3)、如图2，P为y轴正半轴上一动点，连接BP，过点B在x轴下方作BQ⊥BP，且BQ＝BP，连接PC，PQ，QC.在（2）的条件下，设P（0，p），求△PCQ的面积（用含p的式子表示）.

    查看试题解析