河南省周口市鹿邑县2021-2022学年八年级上学期数学教学评价一

试卷更新日期：2021-11-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中属于正多边形的是（）

A、三角形 B、长方形 C、正方形 D、五边形

查看试题解析
2. 如图所示，△ABC 中 AB 边上的高线是（）

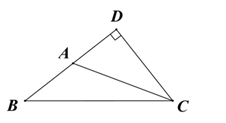A、线段 DA B、线段 CA C、线段 CD D、线段 BD

查看试题解析
3. 如图，点E，F在线段BC上，△ABF与△DCE全等，点A与点D，点B与点C是对应顶点，AF与DE交于点M，则∠DCE=（）

A、∠B B、∠A C、∠EMF D、∠AFB

查看试题解析
4. 有两根木棒的长度分别为20cm和30cm，要钉成一个三角形木架，则下列长度的木棒中不合适的是（）

A、10cm B、20cm C、30cm D、40cm

查看试题解析
5. 下列说法中，正确的结论有（）
①在Rt△ABC中，两个锐角互余；②在两个全等三角形中，对应边相等，对应角相等；③形状相同的两个三角形全等；④三角形的重心是三条角平分线的交点

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，△ABC中，点D在BC延长线上，则下列结论一定成立的是（）

A、∠1＝∠A+∠B B、∠1＝∠2+∠A C、∠1＝∠2+∠B D、∠2＝∠A+∠B

查看试题解析
7. 根据已知条件，能画出唯一三角形的是（）

A、 $A C = 4$ ， $A B = 5$ ， $B C = 10$ B、 $A C = 4$ ， $A B = 5$ ， $∠ B = 60 °$ C、 $∠ A = 50 °$ ， $∠ B = 60 °$ ， $A B = 2$ D、 $∠ C = 90 °$ ， $A B = 5$

查看试题解析
8. 如图， $A D ⊥ B C$ 于点D， $B D = D C$ ，E在AD上，则图中全等的三角形共有几对（）

A、4对 B、3对 C、2对 D、1对

查看试题解析
9. 一个多边形截去一个角后，形成新多边形的内角和为2 520°，则原多边形的边数为（　　）

A、15 B、16 C、13或15 D、15或16或17

查看试题解析
10.
如图所示，∠E=∠F，∠B=∠C，AE=AF，以下结论：①∠FAN=∠EAM；②EM=FN；③△ACN≌△ABM；④CD=DN．其中正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 空调安装在墙上时，一般都采用如图所示的方法固定.这种方法应用的几何原理是：三角形具有.

查看试题解析
12. 在△ABC中， $∠ B = 60 °$ ， $∠ C = 50 °$ ，则 $∠ A =$ .

查看试题解析
13. 如图， $△ A B C ≌ △ D E F$ ，BE=4，AE=1，则DE的长是．

查看试题解析
14. 五边形共有条对角线.

查看试题解析
15. 如图，六边形 $A B C D E F$ 是轴对称图形， $C F$ 所在的直线是它的对称轴，若 $∠ A F C + ∠ B C F = 150^{\circ}$ ，则 $∠ A F E + ∠ B C D$ 的大小是.

查看试题解析
16. 如图，在等腰直角△ABC中， $∠ A B C = 90 °$ ， $A (- 4 ， 0)$ ， $B (0 ， 2)$ ，点C在第四象限，BC与x轴交于点D，则点C的坐标为.

查看试题解析
17. 如图， $△$ ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm，直线l经过点C且与边AB相交.动点P从点A出发沿A→C→B路径向终点B运动；动点Q从点B出发沿B→C→A路径向终点A运动.点P和点Q的速度分别为2cm/s和3cm/s，两点同时出发并开始计时，当点P到达终点B时计时结束.在某时刻分别过点P和点Q作PE⊥l于点E，QF⊥l于点F，设运动时间为t秒，则当t＝秒时， $△$ PEC与 $△$ QFC全等.

查看试题解析

三、解答题

18. 如图所示，已知 $∠ α$ 和线段a，用尺规作一个△ABC，使 $∠ A B C = ∠ α$ ， $A B = a$ ， $B C = 2 a$ .（不写作法，保留作图痕迹）

查看试题解析
19. 一个三角形的三边长分别是xcm、（x+2）cm、（x+5）cm.它的周长不超过37cm.求x的取值范围.

查看试题解析
20. 某段河流的两岸是平行的，数学兴趣小组在老师带领下不用涉水过河就能测得的宽度，他们是这样做的：①在河流的一条岸边B点，选对岸正对的一棵树A；②沿河岸直走20m有一棵树C，继续前行20m到达D处；③从D处沿河岸垂直的方向行走，当到达A树正好被C树遮挡住的E处停止行走；④测得DE的长为5米.

(1)、河的宽度是米.

(2)、请你说明他们做法的正确性.

查看试题解析
21. 如图，△ABC和△DCB有公共边BC，且 $A B = D C$ ，作 $A E ⊥ B C$ ， $D F ⊥ B C$ ，垂足分别为E、F， $A E = D F$ .求证： $A C = B D$ .

查看试题解析
22. 一个多边形除一内角外，其余内角和与外角和之和为1560°.

(1)、求该多边形的边数；

(2)、若该多边形为正多边形，求每一个外角的度数.

查看试题解析
23. 如图，在△ABC中， $∠ A = 30 °$ ， $∠ B = 60 °$ ，CF平分 $∠ A C B$ 交AB于点E.

(1)、求 $∠ A C E$ 的度数：

(2)、若 $C D ⊥ A B$ 于点D， $∠ C D F = 75 °$ .判断△CFD的形状，并说明理由.

查看试题解析
24. 如图，在△ADC中，DB是高，点E是DB上一点， $A B = D B$ ， $E B = C B$ ，M、N分别是AE、CD上的点，且 $A M = D N$ .

(1)、△ABE和△DBC全等吗？请说明理由；

(2)、探索BM与BN之间的数量关系和位置关系，并说明理由.

查看试题解析
25. 如图(1)，已知△ABC中，∠BAC=90⁰ ， AB=AC，AE是过A的一条直线，且B．C在A．E的异侧，BD⊥AE于D，CE⊥AE于E

(1)、试说明：BD=DE+CE.

(2)、若直线AE绕A点旋转到图(2)位置时，其余条件不变，问BD与DE.CE的数量关系如何?请直接写出结果，不需说明

(3)、如图(3)若将图（2）中的AB=AC改为∠ABD=∠ABC其余条件不变，问AD与AE的数量关系如何?并说明理由.

查看试题解析