陕西省宝鸡市金台区2021-2022学年高二上学期数学期中考试试卷

试卷更新日期：2021-11-22 类型：期中考试

进入出卷网下载

一、选择题：本大题共12个小题，每小题5分，共60分.

1. 下列给出的赋值语句中，正确的是（）

A、 $1 = x$ B、 $x = 2$ C、 $a = b = 2$ D、 $x + y = 1$

查看试题解析
2. 宝鸡是一座美丽的城市，为增强市民的环保意识，在6月5日的“世界环境日”活动中，某校以家庭为单位进行了废塑料袋情况的调查.其中，高二（1）班的50名学生在一天中调查了各自家庭丢弃废塑料袋的情况，这个问题中50名学生所在家庭一天丢弃废塑料袋的情况是（）

A、总体 B、样本的数目 C、个体 D、样本

查看试题解析
3. 甲、乙两名运动员的5次测试成绩如图所示，设 $s_{1} ， s_{2}$ 分别表示甲、乙两名运动员测试成绩的标准差， $\bar{x_{1}} ， \bar{x_{2}}$ 分别表示甲、乙两名运动员测试成绩的平均数，则有（）

A、 $\bar{x_{1}} = \bar{x_{2}}$ ， $s_{1} < s_{2}$ B、 $\bar{x_{1}} = \bar{x_{2}}$ ， $s_{1} > s_{2}$ C、 $\bar{x_{1}} > \bar{x_{2}}$ ， $s_{1} > s_{2}$ D、 $\bar{x_{1}} = \bar{x_{2}}$ ， $s_{1} = s_{2}$

查看试题解析
4. 如果 $a ， b ， c$ 满足 $c < b < a$ 且 $a c < 0$ ，那么下列选项中不一定成立的是（）

A、 $a b > a c$ B、 $c (b - a) > 0$ C、 $c b^{2} < a b^{2}$ D、 $a c (a - c) < 0$

查看试题解析
5. 为了测算如图阴影部分的面积，作一个边长为6的正方形将其包含在内，并向正方形内随机投掷800个点，已知恰有200个点落在阴影部分内，据此，可估计阴影部分的面积是（）

A、9 B、12 C、8 D、6

查看试题解析
6. 《算法统宗》是中国古代数学名著，由明代数学家程大位所著，该作完善了珠算口诀，确立了算盘用法，完成了由筹算到珠算的彻底转变.该作中有题为“李白沽酒”(李白街上走，提壶去买酒．遇店加一倍，见花喝一斗，三遇店和花，喝光壶中酒. 借问此壶中，原有多少酒？)，如图为该问题的程序框图，若输出的S值为0，则开始输入的S值为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{5}$ C、 $\frac{7}{8}$ D、 $\frac{15}{16}$

查看试题解析
7. 已知 $3^{a} + 27^{b} = 6$ ，则 $a + 3 b$ 的最大值是（）

A、 $2 \sqrt{3}$ B、6 C、 $2 \sqrt{2}$ D、2

查看试题解析
8. 总体由编号为01，02，…，29，30的30个个体组成，现从中抽取一个容量为6的样本，请从随机数表第1行第5列开始，向右读取，则选出来的第5个个体的编号为（）
70 29 17 12 13 40 33 12 38 26 13 89 51 03

56 62 18 37 35 96 83 50 87 75 97 12 55 93

A、12 B、13 C、03 D、40

查看试题解析
9. 已知实数 $a > b > 0$ ，则下列不等关系中错误的是（）

A、 $\frac{b}{a} < \frac{b + 4}{a + 4}$ B、 $lg \frac{a + b}{2} > \frac{lg a + lg b}{2}$ C、 $a + \frac{1}{b} > b + \frac{1}{a}$ D、 $\sqrt{a} - \sqrt{b} > \sqrt{a - b}$

查看试题解析
10. 某公司有320名员工，将这些员工编号为1，2，3，…，320，从这些员工中使用系统抽样的方法抽取20人进行“学习强国”的问卷调查，若54号被抽到，则下面被抽到的是（）

A、72号 B、150号 C、256号 D、300号

查看试题解析
11. 已知变量 $x$ ， $y$ 满足约束条件 ${\begin{array}{l} 1 \leq x + y \leq 3 \\ - 1 \leq x - y \leq 1 \end{array}$ ，则 $4 x + 2 y$ 的取值范围是（）

A、 $[2 ， 10]$ B、 $[0 ， 12]$ C、 $[0 ， 10]$ D、 $[2 ， 12]$

查看试题解析
12. 关于 $x$ 的不等式 $x^{2} - (a + 1) x + a < 0$ 的解集中，恰有3个整数，则 $a$ 的取值范围是（）

A、 $(4 ， 5)$ B、 $(- 3 ， - 2) \cup (4 ， 5)$ C、 $(4 ， 5]$ D、 $[- 3 ， - 2) \cup (4 ， 5]$

查看试题解析

二、填空题：本大题共4小题，每小题5分，共20分.

13. 已知四个函数：① $y = - x$ ，② $y = - \frac{1}{x}$ ，③ $y = x^{3}$ ，④ $y = x^{\frac{1}{2}}$ ，从中任选2个，则事件“所选2个函数的图象有且仅有一个公共点”的概率为．

查看试题解析
14. 阅读下面的程序，当分别输入 $a = 3$ ， $b = 5$ 时，输出的值 $a =$ ．

查看试题解析
15. 不等式 $\frac{1}{x} < 2$ 的解集为．

查看试题解析
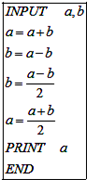16. 一批产品共有100件，其中5件是次品，95件是合格品，从这批产品中任意抽取5件，记 $A$ 为“恰有1件次品”， $B$ 为“至少有2件次品”， $C$ 为“至少有1件次品”， $D$ 为“至多有1件次品”. 现给出下列结论：① $A + B = C$ ；② $B + D$ 是必然事件；③ $A + C = B$ ；④ $A + D = C .$ 其中正确的结论为．（写出序号即可）

查看试题解析

三、解答题：本大题共4小题，共70分.

17. 某校高二（5）班在一次数学测验中，全班 $N$ 名学生的数学成绩的频率分布直方图如下，已知分数在 $110 ～ 120$ 分的学生数有14人．

(1)、求总人数 $N$ 和分数在 $120 ～ 125$ 的人数 $n$ ；

(2)、利用频率分布直方图，估算该班学生数学成绩的众数和中位数各是多少？

(3)、现在从分数在 $115 ～ 120$ 分的学生（男女生比例为1：2）中任选2人，求其中至多含有1名男生的概率．

查看试题解析
18. 下表提供了某厂生产A产品过程中记录的产量 $x$ （吨）与相应的生产能耗 $y$ （吨标准煤）的几组对照数据：

$x$

2

4

6

8

10

$y$

5

6

5

9

10

（参考公式： $\overset{\land}{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n {\bar{x}}_{} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ）

(1)、请根据上表提供的数据，用最小二乘法求出 $y$ 关于 $x$ 的线性回归方程 $\overset{\land}{y} = \overset{\land}{b} x + \overset{\land}{a}$ ；

(2)、根据（1）求出的线性回归方程，预测生产20吨A产品的生产能耗是多少吨标准煤？

查看试题解析
19.

(1)、已知 $a ， b ， c$ 均为正数，且 $a + b + c = 1.$ 证明： $\sqrt{a b} + \sqrt{b c} + \sqrt{a c} \leq 1$

(2)、已知 $x < 3$ ，求 $f (x) = \frac{4}{x - 3} + x$ 的最大值．

查看试题解析
20. 某企业生产甲、乙两种产品，已知生产每吨甲产品要用A原料3吨，B原料2吨；生产每吨乙产品要用A原料1吨，B原料3吨；销售每吨甲产品可获得利润5万元，每吨乙产品可获得利润3万元．该企业在一个生产周期内消耗A原料不超过13吨，B原料不超过18吨．那么在一个生产周期内该企业生产甲、乙两种产品各多少吨可获得最大利润，最大利润是多少？（用线性规划求解要画出规范的图形）

查看试题解析

$x$	2	4	6	8	10
$y$	5	6	5	9	10