北师版数学八年级上册《第七章 平行线的证明》单元检测B卷
试卷更新日期:2021-11-21 类型:单元试卷
一、单选题
-
1. 阅读下列材料,其①~④步中数学依据错误的是( )
如图:已知直线 , ,求证: .
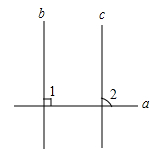
证明:①∵ (已知)
∴ (垂直的定义)
②又∵ (已知)
③∴ (同位角相等,两直线平行)
∴ (等量代换)
④∴ (垂直的定义).
A、① B、② C、③ D、④2. 如图,将一块含有 角的直角三角板放置在两条平行线上,若 ,则 为( )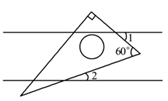 A、 B、 C、 D、3. 将一副直角三角板按如图方式摆放,若直线 ,则 的大小为( )
A、 B、 C、 D、3. 将一副直角三角板按如图方式摆放,若直线 ,则 的大小为( )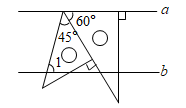 A、 B、 C、 D、4. 如图,直线DE过点A,且 .若 , ,则 的度数为( )
A、 B、 C、 D、4. 如图,直线DE过点A,且 .若 , ,则 的度数为( )
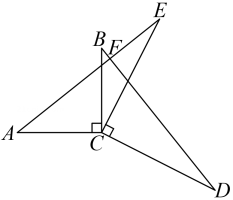
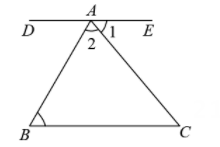 A、 B、 C、 D、5. 如图,点D、E分别在线段 、 上,连接 、 .若 , , ,则 的大小为( )
A、 B、 C、 D、5. 如图,点D、E分别在线段 、 上,连接 、 .若 , , ,则 的大小为( )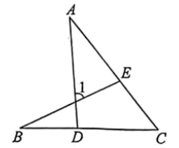 A、60° B、70° C、75° D、85°6. 将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )
A、60° B、70° C、75° D、85°6. 将一副三角尺按如图所示的位置摆放在直尺上,则∠1的度数为( )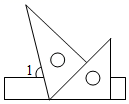 A、45° B、65° C、75° D、85°7. 如图,直线 ,将一个含 角的三角尺按如图所示的位置放置,若 ,则 的度数为( )
A、45° B、65° C、75° D、85°7. 如图,直线 ,将一个含 角的三角尺按如图所示的位置放置,若 ,则 的度数为( ) A、 B、 C、 D、8. 如图,将一副三角尺按图中所示位置摆放,点 在 上,其中 , , , , ,则 的度数是( )
A、 B、 C、 D、8. 如图,将一副三角尺按图中所示位置摆放,点 在 上,其中 , , , , ,则 的度数是( )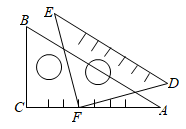 A、 B、 C、 D、9. 一把直尺与一块直角三角板按如图方式摆放,若∠1=47°,则∠2=( )
A、 B、 C、 D、9. 一把直尺与一块直角三角板按如图方式摆放,若∠1=47°,则∠2=( )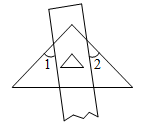 A、40° B、43° C、45° D、47°10. 一块含 角的直角三角板和直尺如图放置,若 ,则 的度数为( )
A、40° B、43° C、45° D、47°10. 一块含 角的直角三角板和直尺如图放置,若 ,则 的度数为( ) A、 B、 C、 D、11. 在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )A、32° B、36° C、40° D、128°12. 如图, , ,垂足为E , 若 ,则 的度数为( )
A、 B、 C、 D、11. 在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )A、32° B、36° C、40° D、128°12. 如图, , ,垂足为E , 若 ,则 的度数为( )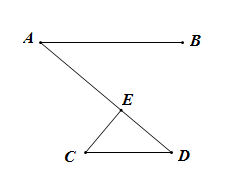 A、40° B、50° C、60° D、90°
A、40° B、50° C、60° D、90°二、填空题
-
13. 如图,已知 , , ,则 .
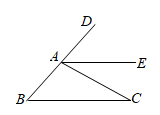 14. 如图,直线 ,点A在直线 上,点 在直线 上, , , ,则 .
14. 如图,直线 ,点A在直线 上,点 在直线 上, , , ,则 . 15. 将一副三角板按如图所示的方式摆放,点D在边AC上, ,则 的大小为度.
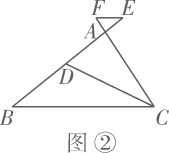
15. 将一副三角板按如图所示的方式摆放,点D在边AC上, ,则 的大小为度.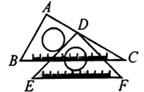 16. 如图,直线a,b过等边三角形 顶点A和C,且 , ,则 的度数为.
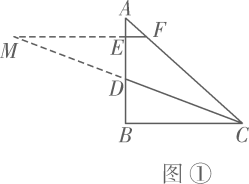
16. 如图,直线a,b过等边三角形 顶点A和C,且 , ,则 的度数为.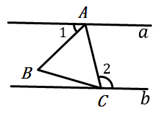 17. 如图,在四边形 中, .设 ,则 (用含 的代数式表示).
17. 如图,在四边形 中, .设 ,则 (用含 的代数式表示).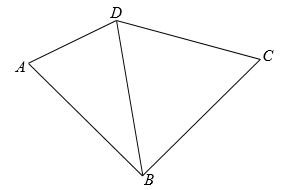 18. 如图,AB∥CD,EF分别与AB,CD交于点B,F,若∠E=30°,∠EFC=130°,则∠A=。
18. 如图,AB∥CD,EF分别与AB,CD交于点B,F,若∠E=30°,∠EFC=130°,则∠A=。
三、解答题
-
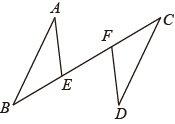
19. 如图,点E、F在线段BC上, , , ,证明: .
 20. 已知:如图,△ABC是任意一个三角形,求证:∠A+∠B+∠C=180°.
20. 已知:如图,△ABC是任意一个三角形,求证:∠A+∠B+∠C=180°.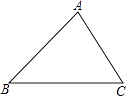 21. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
21. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
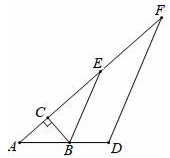 (1)、求∠CBE的度数;
(1)、求∠CBE的度数;
(2)、过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
22. 如图, 是 的外角.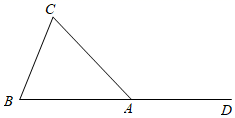 (1)、尺规作图:作 的平分线AE(不写作法,保留作图痕迹,用黑色墨水笔将痕迹加黑);(2)、若 ,求证: .23. 如图, 是 的角平分线,在 上取点 ,使 .
(1)、尺规作图:作 的平分线AE(不写作法,保留作图痕迹,用黑色墨水笔将痕迹加黑);(2)、若 ,求证: .23. 如图, 是 的角平分线,在 上取点 ,使 .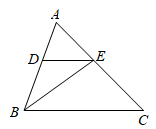 (1)、求证: .(2)、若 , ,求 的度数.
(1)、求证: .(2)、若 , ,求 的度数.