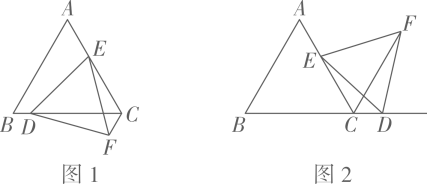北师版数学八年级上册《第七章 平行线的证明》单元检测A卷
试卷更新日期:2021-11-21 类型:单元试卷
一、单选题
-
1. 将一副三角板按如图所示的位置摆放在直尺上,则 的度数为( )
 A、70° B、75° C、80° D、85°2. 如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )
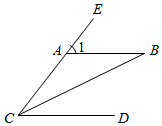
A、70° B、75° C、80° D、85°2. 如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )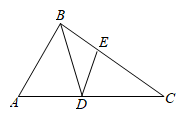 A、30° B、40° C、50° D、60°3. 以下命题是假命题的是( )A、 的算术平方根是2 B、有两边相等的三角形是等腰三角形 C、一组数据:3, ,1,1,2,4的中位数是1.5 D、过直线外一点有且只有一条直线与已知直线平行4. 如图,直线 被直线 所截下列条件能判定 的是( )
A、30° B、40° C、50° D、60°3. 以下命题是假命题的是( )A、 的算术平方根是2 B、有两边相等的三角形是等腰三角形 C、一组数据:3, ,1,1,2,4的中位数是1.5 D、过直线外一点有且只有一条直线与已知直线平行4. 如图,直线 被直线 所截下列条件能判定 的是( )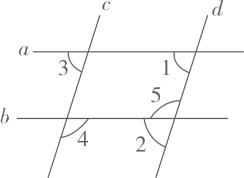 A、 B、 C、 D、5. 如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )
A、 B、 C、 D、5. 如图,AB∥CD,△ACE为等边三角形,∠DCE=40°,则∠EAB等于( )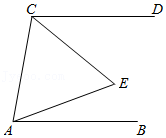 A、40° B、30° C、20° D、15°6. 如图, , ,重足为 , ,则 等于( )
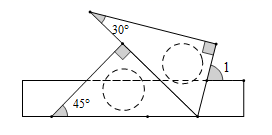
A、40° B、30° C、20° D、15°6. 如图, , ,重足为 , ,则 等于( ) A、40° B、45° C、50° D、60°7. 把一块等腰直角三角板和一把直尺按如图所示的位置构成,若∠1=25°,则∠2的度数为( )
A、40° B、45° C、50° D、60°7. 把一块等腰直角三角板和一把直尺按如图所示的位置构成,若∠1=25°,则∠2的度数为( ) A、15° B、20° C、25° D、30°8. 一副三角板如图就置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中 的度数为( )
A、15° B、20° C、25° D、30°8. 一副三角板如图就置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中 的度数为( )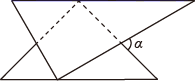 A、45° B、60° C、75° D、85°9. 如图,AM∥BN , ∠ACB=90°,∠MAC=35°,则∠CBN的度数是( )
A、45° B、60° C、75° D、85°9. 如图,AM∥BN , ∠ACB=90°,∠MAC=35°,则∠CBN的度数是( )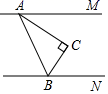 A、35° B、45° C、55° D、65°10. 如图,在△ABC中,AB=AC,分别以点A,B为圆心,大于 AB的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC、AB于点D和点E,若∠B=50°,则∠CAD的度数是( )
A、35° B、45° C、55° D、65°10. 如图,在△ABC中,AB=AC,分别以点A,B为圆心,大于 AB的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC、AB于点D和点E,若∠B=50°,则∠CAD的度数是( )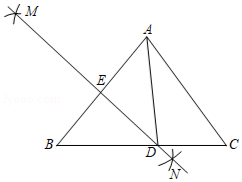 A、30° B、40° C、50° D、60°11. 如图,在Rt△ABC中,∠A=30°,∠C=90°,AB=6,点P是线段AC上一动点,点M在线段AB上,当AM= AB时,PB+PM的最小值为( )
A、30° B、40° C、50° D、60°11. 如图,在Rt△ABC中,∠A=30°,∠C=90°,AB=6,点P是线段AC上一动点,点M在线段AB上,当AM= AB时,PB+PM的最小值为( ) A、3 B、2 C、2 +2 D、3 +312. 如图,直线 的顶点 在 上,若 ,则 ( )
A、3 B、2 C、2 +2 D、3 +312. 如图,直线 的顶点 在 上,若 ,则 ( )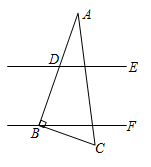 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,AB∥CD,CB平分∠ECD,若∠B=26°,则∠1的度数是.
 14. 如图,在 中,点D、E分别在 、 上, .若 ,则 .
14. 如图,在 中,点D、E分别在 、 上, .若 ,则 .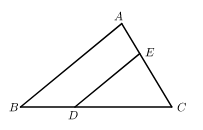 15. 如图,直线 ,一块含有30°角的直角三角尺顶点E位于直线CD上,EG平分 ,则 的度数为°.
15. 如图,直线 ,一块含有30°角的直角三角尺顶点E位于直线CD上,EG平分 ,则 的度数为°.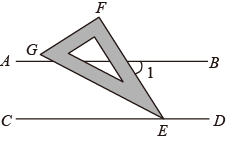 16. 下图是可调躺椅示意图(数据如图), 与 的交点为 ,且 , , 保持不变.为了舒适,需调整 的大小,使 ,则图中 应(填“增加”或“减少”)度.
16. 下图是可调躺椅示意图(数据如图), 与 的交点为 ,且 , , 保持不变.为了舒适,需调整 的大小,使 ,则图中 应(填“增加”或“减少”)度.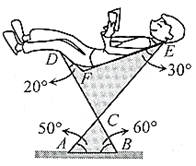 17. 如图,在 中,点D是边BC上的一点.若 , ,则∠C的大小为 .
17. 如图,在 中,点D是边BC上的一点.若 , ,则∠C的大小为 .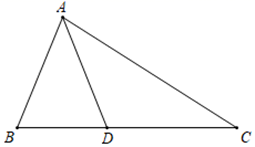 18. 如图.在 中, , .若 ,则 .
18. 如图.在 中, , .若 ,则 .
三、解答题
-
19. 光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射,如图,水面 与水杯下沿 平行,光线 从水中射向空气时发生折射,光线变成 ,点G在射线 上,已知 ,求 的度数.
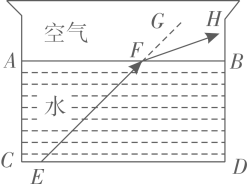 20. 如图,AB∥DE,B,C,D三点在同一条直线上,∠A=90°,EC⊥BD,且AB=CD.求证:AC=CE.
20. 如图,AB∥DE,B,C,D三点在同一条直线上,∠A=90°,EC⊥BD,且AB=CD.求证:AC=CE.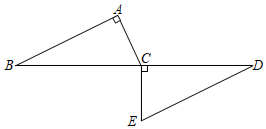 21. 如图,点A、B、D、E在同一条直线上, .求证: .
21. 如图,点A、B、D、E在同一条直线上, .求证: . 22. 如图,在 中, ,点D在边 上,且 ,过点D作 并截取 ,且点C,E在 同侧,连接 .
22. 如图,在 中, ,点D在边 上,且 ,过点D作 并截取 ,且点C,E在 同侧,连接 .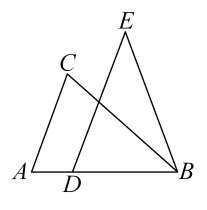
求证: .
23. 如图, 是 的边 上一点, , 交 于 点, . (1)、求证: ≌ ;(2)、若 , ,求 的长.
(1)、求证: ≌ ;(2)、若 , ,求 的长.