北师版数学八年级上册《第六章数据的分析》单元检测A卷

试卷更新日期：2021-11-21 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列说法正确的是（）

A、了解市民知晓“礼让行人”交通新规的情况，适合全面调查 B、一组数据5，5，3，4，1的中位数是3 C、甲、乙两人9次跳高成绩的方差分别为 $S$ _甲² $= 1.1$ ， $S$ _乙² $= 2.5$ ，说明乙的成绩比甲稳定 D、“经过有交通信号灯的路口，遇到红灯”是随机事件

查看试题解析

2. 某校为推荐一项作品参加“科技创新”比赛，对甲、乙、丙、丁四项候选作品进行量化评分，具体成绩（百分制）如表：

项目

作品

甲

乙

丙

丁

创新性

实用性

如果按照创新性占60%，实用性占40%计算总成绩，并根据总成绩择优推荐，那么应推荐的作品是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

3. 某班5名同学参加学校“感党恩，跟党走”主题演讲比赛，他们的成绩（单位：分）分别是8，6，8，7，9，这组数据的中位数是（）

A、6 B、7 C、8 D、9

查看试题解析
4. 若一组数据1，3，4，6，m的平均数为4，则这组数据的中位数和众数分别是（）

A、4，6 B、4，4 C、3，6 D、3，4

查看试题解析
5. 某校健美操队共有10名队员，统计队员的年龄情况，结果如下：13岁3人，14岁5人，15岁2人该健美操队队员的平均年龄为（）

A、14.2岁 B、14.1岁 C、13.9岁 D、13.7岁

查看试题解析
6. 15名学生演讲赛的成绩各不相同，若某选手想知道自己能否进入前8名，则他不仅要知道自己的成绩（）

A、平均数 B、众数 C、方差 D、中位数

查看试题解析
7. 一组数据4，6，x，7，10的众数是7，则这组数据的平均数是（）

A、5 B、6.4 C、6.8 D、7

查看试题解析
8. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示，从图中可以看出这10次测验平均成绩较高且较稳定的是（）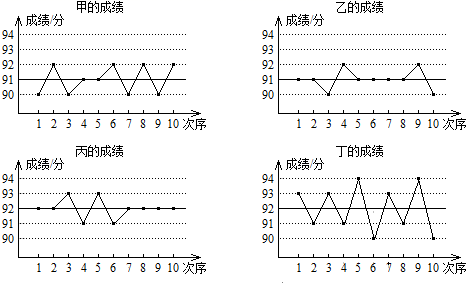

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 为了向建党一百周年献礼，我市中小学生开展了红色经典故事演讲比赛.某参赛小组6名同学的成绩（单位：分）分别为：85，82，86，82，83，92.关于这组数据，下列说法错误的是（）

A、众数是82 B、中位数是84 C、方差是84 D、平均数是85

查看试题解析

10. 为迎接中国共产党建党一百周年，某班50名同学进行了党史知识竞赛，测试成绩统计如下表，其中有两个数据被遮盖．

成绩/分	91	92	93	94	95	96	97	98	99	100
人数	■	■	1	2	3	5	6	8	10	12

下列关于成绩的统计量中，与被遮盖的数据无关的是（）

A、平均数，方差 B、中位数，方差 C、中位数，众数 D、平均数，众数

查看试题解析

11. 下列说法正确的是（）

A、一个不透明的口袋中有3个白球和2个红球（每个球除颜色外都相同），则从中任意摸出一个球是红球的概率为 $\frac{2}{3}$ B、一个抽奖活动的中奖概率为 $\frac{1}{2}$ ，则抽奖2次就必有1次中奖 C、统计甲，乙两名同学在若干次检测中的数学成绩发现： $\bar{x_{甲}} = \bar{x_{乙}}$ ， $S_{甲}^{2} > S_{乙}^{2}$ ，说明甲的数学成绩比乙的数学成绩稳定 D、要了解一个班有多少同学知道“杂交水稻之父”袁隆平的事迹，宜采用普查的调查方式

查看试题解析
12. 如果将一组数据中的每个数都减去5，那么所得的一组新数据（）

A、众数改变，方差改变 B、众数不变，平均数改变 C、中位数改变，方差不变 D、中位数不变，平均数不变

查看试题解析

二、填空题

13. 中药是以我国传统医药理论为指导，经过采集、炮制、制剂而得到的药物.在一个时间段，某中药房的黄芪、焦山楂、当归三种中药的销售单价和销售额情况如下表：

中药	黄芪	焦山楂	当归
销售单价（单位：元/千克）	80	60	90
销售额（单位：元）	120	120	360

则在这个时间段，该中药房的这三种中药的平均销售量为千克.

查看试题解析

14. 黔东南州某校今年春季开展体操活动，小聪收集、整理了成绩突出的甲、乙两队队员（各50名）的身高得到：平均身高（单位：cm）分别为： ${\bar{x}}_{甲}$ ＝160， ${\bar{x}}_{乙} = 162$ ，方差分别为： $S^{2}_{甲} = 1.5$ ， $S^{2}_{乙} = 2.8$ ，现要从甲、乙两队中选出身高比较整齐的一个队参加上一级的体操比赛，根据上述数据，应该选择 .（填写“甲队”或“乙队”）

查看试题解析
15. 若甲、乙两人射击比赛的成绩（单位：环）如下：
甲：6，7，8，9，10；

乙：7，8，8，8，9.

则甲、乙两人射击成绩比较稳定的是（填甲或乙）；

查看试题解析
16. 为庆祝中国共产党建党一百周年，某校开展了主题为“我身边的共产党员”的演讲比赛.比赛从演讲内容、演讲技巧、演讲效果三个方面打分，最终得分按4：3：3的比例计算.若选手甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别为95分、80分、90分，则选手甲的最终得分为分.

查看试题解析

17. 甲乙两班举行一分钟跳绳比赛，参赛学生每分钟跳绳次数的统计结果如表：

班级	参加人数	中位数	方差	平均数
甲	45	109	181	110
乙	45	111	108	110

某同学分析如表后得到如下结论：①甲，乙两班学生平均成绩相同；②乙班优秀人数多于甲班优秀人数（每分钟跳绳≥110次为优秀）；③甲班成绩的波动比乙班大，则正确结论的序号是．

查看试题解析

18. 某外贸公司要出口一批规格为 $200$ 克/盒的红枣，现有甲、乙两个厂家提供货源，它们的价格相同，品质也相近.质检员从两厂的产品中各随机抽取 $15$ 盒进行检测，测得它们的平均质量均为 $200$ 克，每盒红枣的质量如图所示，则产品更符合规格要求的厂家是.（填“甲”或“乙”）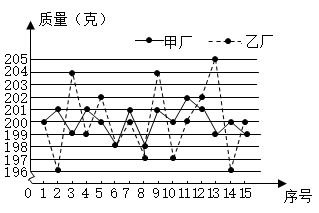

查看试题解析

三、解答题

19. 近5年，我省家电业的发展发生了新变化.以甲、乙、丙3种家电为例，将这3种家电2016～2020年的产量（单位：万台）绘制成如图所示的折线统计图，图中只标注了甲种家电产量的数据.

观察统计图回答下列问题：

(1)、这5年甲种家电产量的中位数为万台；

(2)、若将这5年家电产量按年份绘制成5个扇形统计图，每个统计图只反映该年这3种家电产量占比，其中有一个扇形统计图的某种家电产量占比对应的圆心角大于180°，这个扇形统计图对应的年份是年；

(3)、小明认为：某种家电产量的方差越小，说明该家电发展趋势越好.你同意他的观点吗？请结合图中乙、丙两种家电产量变化情况说明理由.

查看试题解析

20. 某农业科技部门为了解甲、乙两种新品西瓜的品质（大小、甜度等），进行了抽样调查.在相同条件下，随机抽取了两种西瓜各7份样品，对西瓜的品质进行评分（百分制），并对数据进行收集、整理，下面给出两种西瓜得分的统计图表.

甲、乙两种西瓜得分表

序号	1	2	3	4	5	6	7
甲种西瓜（分）	75	85	86	88	90	96	96
乙种西瓜（分）	80	83	87	90	90	92	94

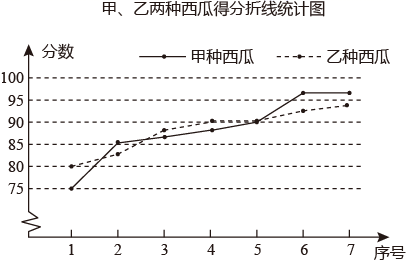
甲、乙两种西瓜得分统计表

	平均数	中位数	众数
甲种西瓜	88	a	96
乙种西瓜	88	90	b

(1)、

a =

，

b =

；

(2)、从方差的角度看，种西瓜的得分较稳定（填“甲”或“乙”）；

(3)、小明认为甲种西瓜的品质较好些，小军认为乙种西瓜的品质较好些.请结合统计图表中的信息分别写出他们的理由.

查看试题解析

21. 2020年我国进行了第七次全国人口普查，小星要了解我省城镇及乡村人口变化情况，根据贵州省历次人口普查结果，绘制了如下的统计图表.请利用统计图表提供的信息回答下列问题：

贵州省历次人口普查城镇人口统计表

年份	1953	1961	1982	1990	2000	2010	2020
城镇人口（万人）	110	204	540	635	845	1175	2050
城镇化率	7%	12%	19%	20%	24%	$a$	53%

贵州省历次人口普查乡村人口统计图

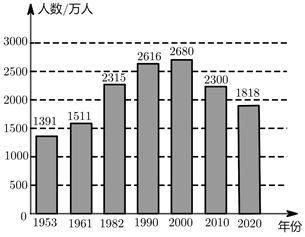(1)、这七次人口普查乡村人口数的中位数是万人；

(2)、城镇化率是一个国家或地区城镇人口占其总人口的百分率，是衡量城镇化水平的一个指标.根据统计图表提供的信息，我省2010年的城镇化率

a

是（结果精确到1%）；假设未来几年我省城乡总人口数与2020年相同，城镇化率要达到60%，则需从乡村迁入城镇的人口数量是.万人（结果保留整数）；

(3)、根据贵州省历次人口普查统计图表，用一句话描述我省城镇化的趋势.

查看试题解析

22. 某水果公司以10元/

kg

的成本价新进2000箱荔枝，每箱质量

5 kg

，在出售荔枝前，需要去掉损坏的荔枝，现随机抽取20箱，去掉损坏荔枝后称得每箱的质量（单位：

kg

）如下：

4.7··4.8·4.6··4.5··4.8··4.9··4.8··4.7··4.8··4.7

4.8··4.9··4.7··4.8··4.5·4.7··4.7··4.9··4.7··5.0

整理数据：							分析数据：
质量（ $kg$ ）	4.5	4.6	4.7	4.8	4.9	5.0	平均数	众数	中位数
数量（箱）	2	1	7	$a$	3	1	4.75	$b$	$c$

(1)、直接写出上述表格中

a

，

b

，

c

的值；

(2)、平均数、众数、中位数都能反映这组数据的集中趋势，请根据以上样本数据分析的结果，任意选择其中一个统计量，估算这

2000

箱荔枝共损坏了多少千克？

(3)、根据（2）中的结果，求该公司销售这批荔枝每千克定为多少元才不亏本？（结果保留一位小数）

查看试题解析

23. 某市在实施居民用水定额管理前，对居民生活用水情况进行了调查，通过简单随机抽样，获得了100个家庭去年的月均用水量数据，将这组数据按从小到大的顺序排列，其中部分数据如下表：

序号	1	2	…	25	26	…	50	51	…	75	76	…	99	100
月均用水量/t	1.3	1.3	…	4.5	4.5	…	6.4	6.8	…	11	13	…	25.6	28

(1)、求这组数据的中位数.已知这组数据的平均数为

9 .2t

，你对它与中位数的差异有什么看法？

(2)、为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费，若要使75%的家庭水费支出不受影响，你觉得这个标准应该定为多少？

查看试题解析

24. 九（1）班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛，在相同的条件下，分别对两名男生进行了八次一分钟跳绳测试.现将测试结果绘制成如下不完整的统计图表，请根据统计图表中的信息解答下列问题：

	平均数	中位数	众数	方差
甲	175	$a$	$b$	93.75
乙	175	175	180，175，170	$c$

(1)、求

a

、

b

的值；

(2)、若九（1）班选一位成绩稳定的选手参赛，你认为应选谁，请说明理由；

(3)、根据以上的数据分析，请你运用所学统计知识，任选两个角度评价甲乙两名男生一分钟跳绳成绩谁优.

查看试题解析

25. 小聪、小明准备代表班级参加学校“党史知识”竞赛，班主任对这两名同学测试了6次，获得如下测试成绩折线统计图.根据图中信息，解答下列问题：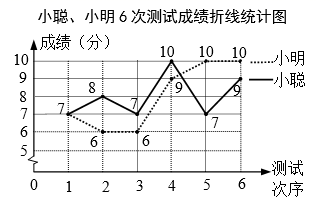

(1)、要评价每位同学成绩的平均水平，你选择什么统计量？求这个统计量.

(2)、求小聪成绩的方差.

(3)、现求得小明成绩的方差为 $S_{小明}^{2} = 3$ （单位：平方分）.根据折线统计图及上面两小题的计算，你认为哪位同学的成绩较好？请简述理由.

查看试题解析

北师版数学八年级上册《第六章 数据的分析》单元检测A卷

一、单选题

二、填空题

三、解答题

北师版数学八年级上册《第六章数据的分析》单元检测A卷