广西防城港市防城区2021-2022学年九年级上学期数学期中试卷
试卷更新日期：2021-11-19 类型：期中考试
一、选择题(共12小题，每小题3分，共36分)
-
1. 如图所示的4个图形中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 在下列关于x的函数中，一定是二次函数的是（ ）。A、y=x2 B、y=ax2+bx+c C、y=8x D、xy=13. 抛物线y=3(x-3)2+4顶点坐标是（ ）．A、(-3，4) B、(3，4) C、(4，3) D、(-4，3)4. 平面直角坐标系内与点P(-1，2)关于原点对称的点的坐标是（ ）A、(2，-1) B、(-1，-2) C、(-2，-1) D、(1，-2)5. 关于x的方程2x2+5=3x中，二次项系数和一次项系数是（ ）A、2，5 B、2，3 C、2，-3 D、-3，26. 二次函数y=x2+x+1与x轴的交点情况是（ ）A、一个交点 B、两个交点 C、三个交点 D、没有交点7. 抛物线y=-2x2经过平移得到y=-2(x+1)2-5，平移方法是（ ）A、向左平移1个单位，再向下平移5个单位 B、向左平移1个单位，再向下平移5个单位 C、向右平移1个单位，再向下平移5个单位 D、向右平移1个单位，再向上平移5个单位8. 如图，把菱形ABOC绕点O顺时针旋转得到菱形DFOE，则下列角中不是旋转角的是（ ）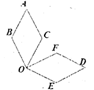
A、∠BOF B、∠AOD C、∠COF D、∠COE9. 用配方法解方程x2+8x+4=0，变形后的结果正确的是（ ）A、(x+4)2=-4 B、(x+4)2=-12 C、(x+4)2=-20 D、(x+4)2=1210. 如图所示，某小区规划在一个长16m，宽9m的矩形场地ABCD上，修建同样宽的小路，使其中两条与AB平行，另一条与AD平行，其余部分种草，如果使草坪部分的总面积为112m2设小路的宽为xcm，那么x满足的方程是（ ）
A、2x2-25x+16=0 B、x2-17x+16=0 C、x2-17x-16=0 D、x2-25x+32=011. 如图，函数y=ax2-2x+1和y=ax-a(a是常数，且a≠0)在同一个平面直角坐标系中的图象可能是（ ）A、
B、
C、
D、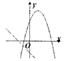
12. 如图，抛物线y=-x2+2x+m+1交x轴于点A(a，0)和B(b，0)，交y轴于点C，抛物线的顶点为D，下列四个命题：①当x>0时，y>0；②若a=-1，则b=5；③抛物线上有两点P(x1 ， y1)和Q(x2 ， y2)，若x1<1<x2 ， 且x1+x2>2， 则y1>y2；④点C关于抛物线对称轴的对称点为E，点G、F分别在x轴和y轴上，当m=2时，四边形EDFG周长的最小值为 ．其中正确的有（ ）个
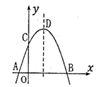A、0 B、1 C、2 D、3二、填空题(共6小题，每题3分，共18分)
-
13. 计算 =14. 若关于x的方程mx2+mx-1=0是一元二次方程，则m的取值范围为15. 已知抛物线y=ax2+1开口向上，且|a|=4，则a= ；16. 时钟上的分针匀速旋转一周需要60分钟，则经过15分钟后，分针旋转了度；17. 如图所示，直线y=mx+n与抛物线y=ax2+bx+c交于A(-1，p)，B(4，q)两点，则关于x的不等式mx+n<ax2+bx+c的解集是
18. 如图，四边形ABCD中，∠BAD=∠C=90°，AB=AD，AE⊥BC，垂足是E，若线段AE=4，则S四边形ABCD=
三、解答题(本大题共8小题，满分66分)
-
19. 用适当的方法解下列方程：(1)、x2-4=0(2)、x2-4x=520. 已知△ABC绕点A逆时针旋转45°得到△ADE，∠BAC=45°，∠C=40°，AB=3，AC=4；
(1)、求∠E和∠EAB的大小；(2)、由旋转的性质得：∠E=∠C=40°， AE=AC=4，旋转角∠EAC=45°，
∴∠EAB=∠EAC+∠BAC=45°+45°=90°；21. 如图，请根据图中信息，求出这个二次函数解析式：
22. 如图，已知△ABC三个顶点的坐标分别是A(-2，3)、B(-6，0)、C(0，0)．
(1)、画出将△ABO关于原点成中心对称的图形△A1B1O，并写出点A的对应点A1的坐标；(2)、画出将△ABO绕坐标原点O逆时针旋转90°得到△A2B2O；(3)、直接写出点A的对应点A2的坐标；以O、A、B、A2为顶点的四边形面积为；23. 已知关于x的一元二次方程x2+4x+2k=0无实数根．(1)、求k的取值范围；(2)、当k取最小整数值时，求该方程的解；(3)、求方程两根的和与积(用k表示)；24. 如图抛物线形拱桥，当拱顶离水面3m时，水面宽6m，连续降雨后，水面上涨1m，水面宽度减少多少？
25. 某中国手机公司在市场销售“China 2021”品牌手机，电于手机价格会随着时间的变化而变化，该手机在第x年(x为整数)的售价y元，y与x满足函数关系式：y=-500x+5000．该公司预计第x年的“China 2021”手机销量为z (百万台)， z与x的对应关系如表(满足一次函数关系)：第x年
1
2
3
4
5
……
销售量z (百万台)
14
16
18
20
22
……
(1)、求z与x的函数关系式；(2)、设第x年的“China 2021手机的年销售额为W (百万元)，试问该公司销售“China 2021"”手机在第几年的年销售额可以达到最大？最大值为多少百万元？(3)、若生产一台"“China 2021”手机的成本为3000元，如果你是该公司的决策者，要使得公司的累计总利润最大(当该年的手机利润为零时)，公司就停产该手机，那么“China 2021”手机销售几年就应该停产去生产新的手机？26. 如图，抛物线y=ax2+bx+2交x轴于点A(-3，0)和点B(1，0)，交y轴于点C．
(1)、求该抛物线的解析式；(2)、点D的坐标为(-1，0)，点P为第二象限内抛物线上的一个动点，求四边形ADCP面积的最大值：(3)、抛物线对称轴上是否存在点M，使△MAB以AB为斜边的直角三角形，若存在，请直接写出点M的坐标；若不存在，并说明理由．