山东省泰安市高新区2021-2022学年七年级上学期数学期中试卷（五四学制）
试卷更新日期：2021-11-19 类型：期中考试
一、选择题(本大题共12小题，每小题选对得4分)
-
1. 下列图形是一些航空公司的标志，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 如图所示，△ABC的边AC上的高是（ ）
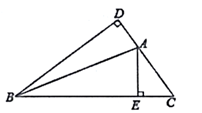A、线段AE B、线段BA C、线段BD D、线段DA3. 如图，△ACB≌△A'CB'，∠A'CB=30°，∠ACB'=110°，则∠ACA'的度数是（ ）
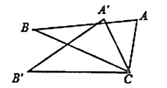A、20° B、30° C、35° D、40°4. 在△ABC中，有下列条件：①∠A+∠B=∠C；②∠A：∠B：∠C=1：2：3；③∠A=2∠B=3∠C；④∠A=∠B= ∠C．其中能确定△ABC是直角三角形的条件有（ ）A、1个 B、2个 C、3个 D、4个5. 如图，在Rt△ABC中，∠ACB=90°，AE为△ABC的角平分线，且ED⊥AB，若AC=6，BC=8，则BD的长（ ）
A、5 B、4 C、3 D、26. 有四根细木棒，长度分别为3cm，5cm，7cm，9cm，从中任取三根拼成三角形，则所拼得的三角形的周长不可能是（ ）A、21cm B、17cm C、19cm D、15cm7. 如图，在△ABC和△CDE中，点B、D、C在同一直线上，已知∠ACB=∠E， AC=CE，添加以下条件后，仍不能判定△ABC≌△CDE的是（ ）
A、∠A=∠DCE B、AB∥DE C、BC=DE D、AB=CD8. 如图，在直角△ABC中，∠C=90°，AB的垂直平分线交AB于D，交AC于E，且∠EBC=2∠EBA，则∠A等于（ ）
A、20° B、22.5° C、25° D、27.5°9. 如图，已知△ABC，求作一点P，使P到∠A的两边的距离相等，且PA=PB．下列确定P点的方法正确的是（ ）
A、P为∠A，∠B两角平分线的交点． B、P为CA的角平分线与AB的垂直平分线的交点 C、P为AB，AC两边上的高的交点 D、P为AB，AC两边的垂直平分线的交点，10. 如图，∠AOC=∠BOC=10°，OC=20，在OA上找一点M，在OB上找一点N，则CM+MN的最小值是（ ）
A、10 B、12 C、16 D、2011. 有一张直角三角形纸片，两直角边AC=6cm，BC=8cm，将△ABC折叠，使点B与点A重合，折痕为DE（如图），则CD等于（ ）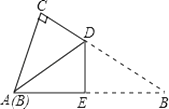
A、 B、 C、 D、12. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为8cm，则图中所有正方形的面积的和是（ ）
A、192cm2 B、64cm2 C、128cm2 D、81cm2二、 填空题(本大题共6小题，满分24分，每小题填对得4分)
-
13. 若(a-3)2+|7-b|=0，则以a、b为边长的等腰三角形的周长为 ．14. 如图，在Rt△ABC中，∠C=90°，∠B=30°，AD是△ABC的角平分线，CD=2，则BC= ．
15. 如图，已知△ABC≌△ADE，∠C=79°，DE⊥AB，则∠D的度数为
16. 如图，在△ABC中，AB=AC，BD是∠ABC的平分线，DE∥AB与BC边相交于点E，若BE=3，CE=5，则△CDE的周长是 ．
17. 如图，一个三级台阶，它的每一级的长宽和高分别为20、3、2，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是
18. 如图，在△ABC中，过点A作∠BAC的角平分线交BC于P，CM⊥AP于N．若∠CAB=30° ，∠B=55°，则∠BPM=
三、解答题(共7小题，满分78分．)
-
19. 如图，△ABC的三个顶点都在格点上，每个小方格的边长为1．
⑴请求出△ABC的面积。
⑵画出△ABC关于y轴对称的△A1B1C1；
⑶在x轴上找一点P，使△PBC的周长最小． (标出点P即可)
20. 如图，在△ABC中，D、E是边BC上两点，且∠ADC=∠AEB，∠B=∠C，求证：△BAD≌△CAE．
21. 上午8时，一条船从港口A出发，以15海里/时的速度向正北方向航行，10时到达海岛B处，从A，B两处望灯塔C，分别测得∠NAC=15°，∠NBC=30°．若该船从海岛B继续向正北航行，求船与灯塔C的最短距离．
22. 如图，AD平分∠BAC，点F在DA的延长线上，FE⊥BC，∠B=38°，∠C=64°。求∠DFE的度数；
23. 有一架秋千，当它静止时，踏板离地的垂直高度DE=0.5m，将它往前推送2m(水平距离BC=2m)时，秋千的踏板离地的垂直高度BF=1.5m，秋千的绳索始终拉得很直，求绳索AD的长度
