山东省泰安市岱岳区2021-2022学年七年级上学期数学期中试卷
试卷更新日期:2021-11-19 类型:期中考试
一、单选题
-
1. 现实世界中,对称现象无处不在,中国的方块字中有些也只有对称性,下列汉字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列线段能构成三角形的是( )A、4,5,6 B、6,7,15 C、4,7,12 D、5,9,143. 已知等腰三角形的一个角为75°,则其顶角为( )A、30° B、75° C、105° D、30°或75°4. 在下列说法中,正确的个数有( ).
2. 下列线段能构成三角形的是( )A、4,5,6 B、6,7,15 C、4,7,12 D、5,9,143. 已知等腰三角形的一个角为75°,则其顶角为( )A、30° B、75° C、105° D、30°或75°4. 在下列说法中,正确的个数有( ).①三角对应相等的两个三角形全等 ②两角、一边对应相等的两个三角形全等
③三边对应相等的两个三角形全等 ④两边、一角对应相等的两个三角形全等
A、1个 B、2个 C、3个 D、4个5. 如图,若 与 关于直线 对称, 交 于点 ,则下列说法中,不一定正确的是( )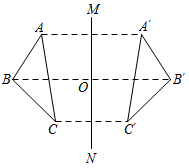 A、 B、 C、 D、6. 如图, ,点A和点B , 点C和点D是对应点.如果 , ,那么 度数是( )
A、 B、 C、 D、6. 如图, ,点A和点B , 点C和点D是对应点.如果 , ,那么 度数是( )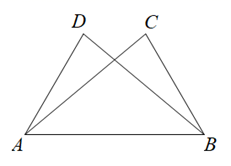 A、80° B、70° C、60° D、50°7. 如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
A、80° B、70° C、60° D、50°7. 如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )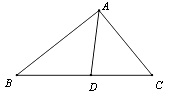 A、3:4 B、4:3 C、16:9 D、9:168. 下列能断定△ABC为等腰三角形的是( )A、∠A=30º、∠B=60º B、∠A=50º、∠B=80º C、AB=AC=2,BC=4 D、AB=3、BC=7,周长为139. 下列各组线段中,能构成直角三角形的一组是( )A、1,2, 3 B、6,8,12 C、3,4,6 D、40,50,3010. 如图,AB与CD相交于点E,AD=CB,要使△ADE≌△CBE,需添加一个条件,则添加的条件以及相应的判定定理正确的是( )
A、3:4 B、4:3 C、16:9 D、9:168. 下列能断定△ABC为等腰三角形的是( )A、∠A=30º、∠B=60º B、∠A=50º、∠B=80º C、AB=AC=2,BC=4 D、AB=3、BC=7,周长为139. 下列各组线段中,能构成直角三角形的一组是( )A、1,2, 3 B、6,8,12 C、3,4,6 D、40,50,3010. 如图,AB与CD相交于点E,AD=CB,要使△ADE≌△CBE,需添加一个条件,则添加的条件以及相应的判定定理正确的是( )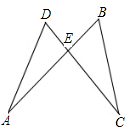 A、AE=CE;SAS B、DE=BE;SAS C、∠D=∠B;AAS D、∠A=∠C;ASA11. 如图,在 中分别以三角形的三条边为边向外作正方形,面积分别记为 , , ,若 , ,则 的值为( )
A、AE=CE;SAS B、DE=BE;SAS C、∠D=∠B;AAS D、∠A=∠C;ASA11. 如图,在 中分别以三角形的三条边为边向外作正方形,面积分别记为 , , ,若 , ,则 的值为( )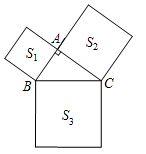 A、10 B、6 C、12 D、2012. 如图,OD平分∠AOB,DE⊥AO于点E,DE=4,点F是射线OB上的任意一点,则DF的长度不可能是( )
A、10 B、6 C、12 D、2012. 如图,OD平分∠AOB,DE⊥AO于点E,DE=4,点F是射线OB上的任意一点,则DF的长度不可能是( )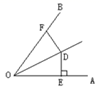 A、3 B、4 C、5 D、613. 如图为了测量B点到河对而的目标A之间的距离,在B点同侧选择了一点C , 测得 , ,然后在M处立了标杆,使 , ,得到 ,所以测得 的长就是A , B两点间的距离,这里判定 的理由是( )
A、3 B、4 C、5 D、613. 如图为了测量B点到河对而的目标A之间的距离,在B点同侧选择了一点C , 测得 , ,然后在M处立了标杆,使 , ,得到 ,所以测得 的长就是A , B两点间的距离,这里判定 的理由是( )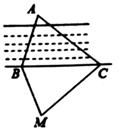 A、 B、 C、 D、14. 等腰三角形的周长为16,其一边长为4.那么它们的底边长为( )A、5 B、4 C、8 D、4或815. 一根长 的吸管插入底面直径为 ,高为 的圆柱形饮料杯中,吸管露在杯子外面的长度为h , 则h的值不可能是( )A、 B、 C、 D、16. 如图,在△ABC中,∠C=90°,AD平分∠BAC , DE⊥AB于E,下列结论:① ;② ;③∠BDE=∠BAC;④BE=DE;⑤ ,其中正确的个数为( )
A、 B、 C、 D、14. 等腰三角形的周长为16,其一边长为4.那么它们的底边长为( )A、5 B、4 C、8 D、4或815. 一根长 的吸管插入底面直径为 ,高为 的圆柱形饮料杯中,吸管露在杯子外面的长度为h , 则h的值不可能是( )A、 B、 C、 D、16. 如图,在△ABC中,∠C=90°,AD平分∠BAC , DE⊥AB于E,下列结论:① ;② ;③∠BDE=∠BAC;④BE=DE;⑤ ,其中正确的个数为( ) A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
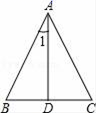
17. 如图,已知:AB=AC , D是BC边的中点,则∠1+∠C=度.
 18. 如图, ,CE=6,FC=2,则BE= .
18. 如图, ,CE=6,FC=2,则BE= .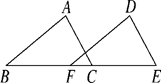 19. 如图,已知OC平分∠AOB,CD//OB,若OD=3cm,则CD=cm.
19. 如图,已知OC平分∠AOB,CD//OB,若OD=3cm,则CD=cm. 20. 如图,长为 的橡皮筋放置在桌面上,固定两端A和B , 然后把皮筋中点竖直向上抬升 到C , 则橡皮筋的长度比原来长了cm.
20. 如图,长为 的橡皮筋放置在桌面上,固定两端A和B , 然后把皮筋中点竖直向上抬升 到C , 则橡皮筋的长度比原来长了cm. 21. 小明从家匀速走到邮局用了8分钟,然后右转弯用同样的速度走了6分钟到达书店(如图所示).已知书店距离邮局660米,那么小明家距离书店米.
21. 小明从家匀速走到邮局用了8分钟,然后右转弯用同样的速度走了6分钟到达书店(如图所示).已知书店距离邮局660米,那么小明家距离书店米.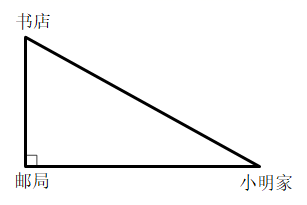 22. 如图所示ΔABC中,AB=AC=14cm,AB的垂直平分线MN交AC于D,ΔDBC的周长是24cm,则BC=cm.
22. 如图所示ΔABC中,AB=AC=14cm,AB的垂直平分线MN交AC于D,ΔDBC的周长是24cm,则BC=cm.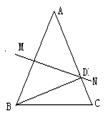
三、解答题
-
23. 如图,在 中, , 于D , E是 上的一点, 交 的延长线于F . 求证: .
 24. 如图,点 B 为 AC 上一点,AD//CE,∠ADB = ∠CBE,BD = EB
24. 如图,点 B 为 AC 上一点,AD//CE,∠ADB = ∠CBE,BD = EB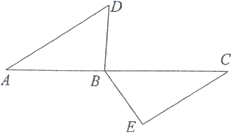
求证:
(1)、△ABD≌△CEB;(2)、AC = AD+ CE.25. 某大学计划为新生配备如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB和CD的长相等,O是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD设计为30 cm,由以上信息能求出CB的长度吗?请你说明理由.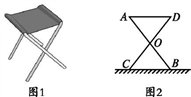 26. 如图,已知在等边三角形ABC中,D、E分别是AB、AC上的点,且AD=CE . 求证:CD=BE .
26. 如图,已知在等边三角形ABC中,D、E分别是AB、AC上的点,且AD=CE . 求证:CD=BE .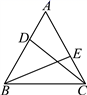 27. 如图,在 中, , 平分 交 于点D , 过点D作 于点E .
27. 如图,在 中, , 平分 交 于点D , 过点D作 于点E .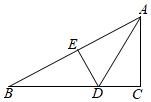 (1)、求证: .(2)、若 , ,求 的长.
(1)、求证: .(2)、若 , ,求 的长.