山东省青岛市莱西市2021-2022学年七年级上学期数学期中试卷
试卷更新日期:2021-11-19 类型:期中考试
一、单选题
-
1. 下面图形中,是轴对称图形的是( )A、
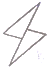 B、
B、 C、
C、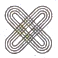 D、
D、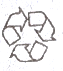 2. 下列四个选项中,不是全等图形的是( )A、
2. 下列四个选项中,不是全等图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列三角形是直角三角形的是( )A、
3. 下列三角形是直角三角形的是( )A、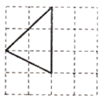 B、
B、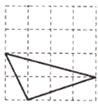 C、
C、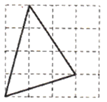 D、
D、 4. 一个三角形的两边长分别为3和8,则它的第三边长可能是( )A、5 B、12 C、8 D、无法确定5. 下列条件不能得到等边三角形的是( )A、有一个内角是60°的锐角三角形 B、有一个内角是60°的等腰三角形 C、顶角和底角相等的等腰三角形 D、腰和底边相等的等腰三角形6. 下列所叙述的图形中,全等的两个三角形是( )A、含有45°角的两个直角三角形 B、腰相等的两个等腰三角形 C、边长相等的两个等边三角形 D、一个钝角对应相等的两个等腰三角形7. 如图所示,在 中,分别以三角形的三条边为边向外作正方形,面积分别记为 , , ,若 , ,则 的值为( )
4. 一个三角形的两边长分别为3和8,则它的第三边长可能是( )A、5 B、12 C、8 D、无法确定5. 下列条件不能得到等边三角形的是( )A、有一个内角是60°的锐角三角形 B、有一个内角是60°的等腰三角形 C、顶角和底角相等的等腰三角形 D、腰和底边相等的等腰三角形6. 下列所叙述的图形中,全等的两个三角形是( )A、含有45°角的两个直角三角形 B、腰相等的两个等腰三角形 C、边长相等的两个等边三角形 D、一个钝角对应相等的两个等腰三角形7. 如图所示,在 中,分别以三角形的三条边为边向外作正方形,面积分别记为 , , ,若 , ,则 的值为( )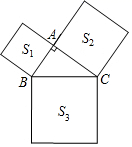 A、17 B、20 C、25 D、318. 如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=100°,则∠ACB的度数为( )
A、17 B、20 C、25 D、318. 如图,四边形ABCD中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=100°,则∠ACB的度数为( )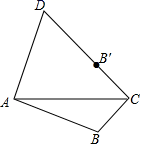 A、40° B、45° C、60° D、80°
A、40° B、45° C、60° D、80°二、填空题
-
9. 如图所示,其中与甲成轴对称的图形是 .
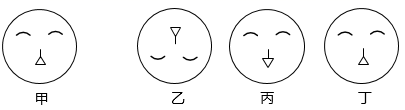 10. 在等腰 ABC中,AB=AC,∠B=50°,则∠A的大小为 .11. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了米.
10. 在等腰 ABC中,AB=AC,∠B=50°,则∠A的大小为 .11. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了米.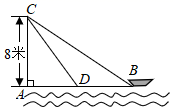 12. 如图,Rt△ABC中,∠C=90°,利用尺规在BC , BA上分别截取BE , BD , 使BE=BD;分别以D , E为圆心、以大于 DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若CG=1,P为AB上一动点,则GP的最小值为 .
12. 如图,Rt△ABC中,∠C=90°,利用尺规在BC , BA上分别截取BE , BD , 使BE=BD;分别以D , E为圆心、以大于 DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若CG=1,P为AB上一动点,则GP的最小值为 .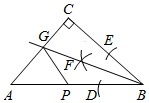 13. 如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为.
13. 如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为.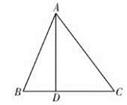 14. 如图,线段AB、BC的垂直平分线 、 相交于点O,若 39°,则 = .
14. 如图,线段AB、BC的垂直平分线 、 相交于点O,若 39°,则 = .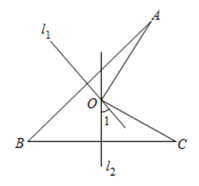 15. 如图,在 中, , ,AB的垂直平分线交BC于D , 交AB于E , 若 ,则 cm.
15. 如图,在 中, , ,AB的垂直平分线交BC于D , 交AB于E , 若 ,则 cm.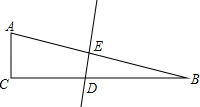 16. 如图,已知长方体的长 ,宽 ,高 ,一只蚂蚁如果沿长方体的表面从A点爬到 点,最短路程是cm.
16. 如图,已知长方体的长 ,宽 ,高 ,一只蚂蚁如果沿长方体的表面从A点爬到 点,最短路程是cm.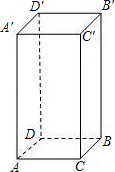
三、解答题
-
17. 已知:线段a , b和 ,求作: ,使 , , .
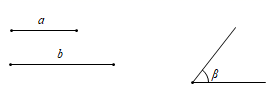 18. 如图,已知 ,BD是 的平分线,那么 是等腰三角形吗?为什么?
18. 如图,已知 ,BD是 的平分线,那么 是等腰三角形吗?为什么?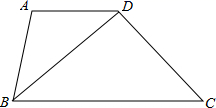 19. 如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm,求BC的长.
19. 如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm,求BC的长.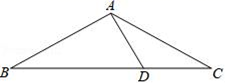 20. 如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.
20. 如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.求证:△BED≌△CFD.
 21. 一船在灯塔C正东方向4海里的A处,以30海里/时的速度沿西偏北60°方向航行.多长时间,船到达灯塔的正北?22. 两个大小不同的等腰直角三角形三角板如图1所示位置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连结DC.
21. 一船在灯塔C正东方向4海里的A处,以30海里/时的速度沿西偏北60°方向航行.多长时间,船到达灯塔的正北?22. 两个大小不同的等腰直角三角形三角板如图1所示位置,图2是由它抽象出的几何图形,B、C、E在同一条直线上,连结DC.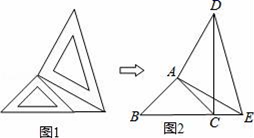 (1)、请找出图2中的全等三角形,并说明理由(说明:结论中不得有未标识的字母);(2)、判断DC⊥BE是否成立?说明理由.23. 某校七年级班学生到野外活动,为测量一池塘两端A、B之间的距离,设计出如下几种方案:
(1)、请找出图2中的全等三角形,并说明理由(说明:结论中不得有未标识的字母);(2)、判断DC⊥BE是否成立?说明理由.23. 某校七年级班学生到野外活动,为测量一池塘两端A、B之间的距离,设计出如下几种方案: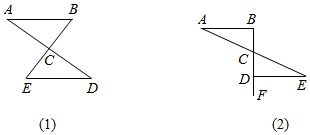
方案a:如图(1)所示,先在平地上取一个可直接到达A、B的点C , 再连接AC、BC , 并分别延长AC至D , BC至E , 使 , ,最后测出DE的距离即为AB之长:
方案b:如图(2)所示,过点B作AB的垂线BF , 再在BF上取C、D两点,使 ,接着过点D作BD的垂线DE , 交AC的延长线于点E , 则测出了DE的长即为A、B之间的距离.
阅读后回答下列问题:
(1)、方案a是否可行?请说明理由(2)、方案b是否可行?不必说明理由(3)、方案b中作 , 的目的是_ ▲ _,若仅满足 ,方案b的结论是否成立.24. 如图,在长方形ABCD中 , ,延长BC到E , 使 ,连接DE . 动点P从点B出发,以每秒2个单位的速度沿 向终点A运动,设点P运动的时间为t秒,存在这样的t , 使 和△DCE全等,则t的值为多少?