河北省唐山市迁安市2021-2022学年七年级上学期数学期中试卷
试卷更新日期:2021-11-19 类型:期中考试
一、单选题
-
1. 向东行驶3km,记作+3km,向西行驶2km记作( )A、+2km B、﹣2km C、+3km D、﹣3km2. - 是一个数的相反数,这个数是( )A、2 B、-2 C、 D、-3. 若 ,则 的值为( )A、 B、1 C、5 D、4. 根据直线、射线、线段的性质,图中的各组直线、射线、线段一定能相交的是( )A、
 B、
B、 C、
C、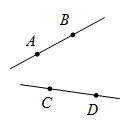 D、
D、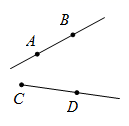 5. 下列说法正确的是( )A、角的大小和开口的大小无关 B、互余、互补是指两个角之间的数量关系 C、单独的一个角也可以叫余角或补角 D、若三个角的和是直角,则他们互余6. 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )
5. 下列说法正确的是( )A、角的大小和开口的大小无关 B、互余、互补是指两个角之间的数量关系 C、单独的一个角也可以叫余角或补角 D、若三个角的和是直角,则他们互余6. 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( ) A、25° B、35° C、45° D、55°7. 如图,若A是实数a在数轴上对应的点,则关于a,-a,1的大小关系表示正确的是( )
A、25° B、35° C、45° D、55°7. 如图,若A是实数a在数轴上对应的点,则关于a,-a,1的大小关系表示正确的是( ) A、 B、 C、 D、8. 在直线a上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB的长度是( )A、2cm B、0.5cm C、1.5cm D、1cm9. 下面等式成立的是( )A、83.5°=83°50′ B、37°12′36″=37.48° C、24°24′24″=24.44° D、41.25°=41°15′10. 当分针指向12,时针这时恰好与分针成30°的角,此时是( )A、9点钟 B、10点钟 C、11点钟或1点钟 D、2点钟或10点钟11. 小明做了以下4道计算题:①(-1)2020+(-2)=-3;②0-(-1)=1;③- ;④ ÷(- )=-1.请你帮他检查一下,他一共做对了( )A、4 题 B、3题 C、2题 D、1题12. 如图,将 就点C按逆时针方向旋转75°后得到 ,若∠ACB=25°,则∠BCA′的度数为( )
A、 B、 C、 D、8. 在直线a上顺次取A、B、C三点,使得AB=5cm,BC=3cm,如果O是线段AC的中点,那么线段OB的长度是( )A、2cm B、0.5cm C、1.5cm D、1cm9. 下面等式成立的是( )A、83.5°=83°50′ B、37°12′36″=37.48° C、24°24′24″=24.44° D、41.25°=41°15′10. 当分针指向12,时针这时恰好与分针成30°的角,此时是( )A、9点钟 B、10点钟 C、11点钟或1点钟 D、2点钟或10点钟11. 小明做了以下4道计算题:①(-1)2020+(-2)=-3;②0-(-1)=1;③- ;④ ÷(- )=-1.请你帮他检查一下,他一共做对了( )A、4 题 B、3题 C、2题 D、1题12. 如图,将 就点C按逆时针方向旋转75°后得到 ,若∠ACB=25°,则∠BCA′的度数为( ) A、50° B、40° C、25° D、60°13. 下面出示的的尺规作图题,题中符号代表的内容正确的是( )
A、50° B、40° C、25° D、60°13. 下面出示的的尺规作图题,题中符号代表的内容正确的是( )如图,已知∠AOB,求作:∠DEF,使∠DEF=∠AOB
作法:
⑴以①为圆心,任意长为半径画弧,分别交OA、OB于点P、Q;
⑵作射线EG,并以点E为圆心②长为半径画弧交EG于点D;
⑶以点D为圆心③长为半径画弧交(2)步中所画弧于点F;
⑷作④,∠DEF即为所求作的角.
 A、①表示点E B、②表示PQ C、③表示OQ D、④表示射线EF14. 在算式3-|-1□2|中的“□”里,选择一个运算符号,使得算式的值最大( )A、+ B、- C、× D、÷15. 如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若∠ABF 比 ∠EBF大15°,则∠EBC的度数是( )
A、①表示点E B、②表示PQ C、③表示OQ D、④表示射线EF14. 在算式3-|-1□2|中的“□”里,选择一个运算符号,使得算式的值最大( )A、+ B、- C、× D、÷15. 如图,在正方形ABCD中,E为DC边上一点,沿线段BE对折后,若∠ABF 比 ∠EBF大15°,则∠EBC的度数是( ) A、15度 B、20度 C、25度 D、30度16. 如图,∠AOB=α , OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线,…,OAn、分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn的度数是( )
A、15度 B、20度 C、25度 D、30度16. 如图,∠AOB=α , OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线,…,OAn、分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 如果a、b互为倒数,c、d互为相反数,且 ,则 .18. 如图所示,C、D是线段AB上两点,若AC=3,C为线段AD中点且AB=10,则线段DB长是.
 19. 数学家发明了一个魔术盒,当任意数对(a,b)放入其中时,会得到一个新的数:a2+b+1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)+1=8.现将数对(﹣2,3)放入其中得到数m= , 再将数对(m,1)放入其中后,得到的数是 .
19. 数学家发明了一个魔术盒,当任意数对(a,b)放入其中时,会得到一个新的数:a2+b+1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)+1=8.现将数对(﹣2,3)放入其中得到数m= , 再将数对(m,1)放入其中后,得到的数是 .三、解答题
-
20.(1)、计算:11-18-12+ 19(2)、计算: -12+2014×(- )×0-(-3)21.(1)、( )×(-48)(2)、-32- [(-5)2×(- )-240÷(-4)× ]22. 如图,已知线段AB , 按下列要求完成画图和计算:
 (1)、延长线段AB到点C , 使BC=3AB(尺规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,如果点D为线段BC的中点,且AB=2,求线段AD的长度;(3)、在以上的条件下,若点P从A点出发,以每秒1个单位长度的速度向点C移动,到点C时停止.设点P的运动时间为t秒,是否存在某时刻t , 使得PB=PA﹣PC?若存在,求出时间t:若不存在,请说明理由.23. 某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下.(单位:km)
(1)、延长线段AB到点C , 使BC=3AB(尺规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,如果点D为线段BC的中点,且AB=2,求线段AD的长度;(3)、在以上的条件下,若点P从A点出发,以每秒1个单位长度的速度向点C移动,到点C时停止.设点P的运动时间为t秒,是否存在某时刻t , 使得PB=PA﹣PC?若存在,求出时间t:若不存在,请说明理由.23. 某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下.(单位:km)第一次
第二次
第三次
第四次
第五次
第六次
第七次
﹣4
+7
﹣9
+8
+6
﹣5
﹣2
(1)、求收工时距A地多远?(2)、在第几次记录时距A地最远?(3)、若每km耗油0.3升,问共耗油多少升?24. 如图所示,观察数轴,请回答. (1)、点C与点D的距离为 , 点B与点D的距离为;点B与点E的距离为 , 点C与点A的距离为;(2)、发现:在数轴上,如果点M与点N分别表示数m , n , 则它们之间的距离可表示为MN=(用m , n表示);(3)、利用发现的结论,逆向思维解决下列问题:
(1)、点C与点D的距离为 , 点B与点D的距离为;点B与点E的距离为 , 点C与点A的距离为;(2)、发现:在数轴上,如果点M与点N分别表示数m , n , 则它们之间的距离可表示为MN=(用m , n表示);(3)、利用发现的结论,逆向思维解决下列问题:①数轴上表示x的点P与 B之间的距离是1,则x的值是 ▲ ;
②|x+3|=2,则x= ▲ ;
③数轴上是否存在点P , 使点P到点B、点C的距离之和为11?若存在,请求出x的值;若不存在,说明理由.
25. 如图1,把直角三角形MON的直角顶点O 放在直线AB上,射线 OC平分∠AON . (1)、观察分析:
(1)、观察分析:
如图1,若∠MOC=28°,则∠BON的度数为;(2)、若将三角形MON绕点O旋转到如图2所示的位置,若∠BON=100°,求∠MOC 的度数.(3)、猜想探究:若将三角形 MON绕点O旋转到如图3所示的位置,请你猜想∠BON和∠MOC之间的数量关系,并说明理由.