河北省唐山市路北区2021-2022学年七年级上学期数学期中试卷

试卷更新日期：2021-11-19 类型：期中考试

进入出卷网下载

一、单选题

1. 如果温度上升3℃，记作+3℃，那么温度下降2℃记作（）

A、-2℃ B、+2℃ C、+3℃ D、-3℃

查看试题解析
2. 已知A地的海拔高度为-36米，B地比A地高20米，则B地的海拔高度为（）

A、16米 B、20米 C、-16米 D、-56米

查看试题解析
3. 在数 $- (- 3)$ ，0， ${(- 3)}^{2}$ ， $| - 9 |$ ， $- 1^{4}$ 中，正数的个数为（）

A、2 B、3 C、4 D、5

查看试题解析
4. 下列各组是同类项的一组是（）

A、 $5 x y$ 与 $2 x y z$ B、2与-7 C、 $- 2 x^{2} y$ 与 $5 y^{2} z$ D、 $3 a c$ 与 $7 b c$

查看试题解析
5. 下列说法正确的是（）

A、 $- 2^{3}$ 的底数是-2 B、 $2 \times 3^{2}$ 的底数是 $2 \times 3$ C、 ${(- 3)}^{4}$ 的底数是-3，指数是4 D、 $- 3^{4}$ 的幂是-12

查看试题解析
6. 在算式 $1 - | - 2 □ 3 |$ 中，“□”内填入下列运算符号中的一种，计算结果最大的是（）

A、+ B、- C、× D、÷

查看试题解析
7. 如图，在数轴上，小手遮挡住的点表示的数可能是（）

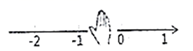A、-1.5 B、-2.5 C、-0.5 D、0.5

查看试题解析
8. 一个多项式与 $x^{2} - 2 x + 1$ 的和是 $3 x - 2$ ，则这个多项式为（）

A、 $x^{2} - 5 x + 3$ B、 $- x^{2} + x - 1$ C、 $- x^{2} + 5 x - 3$ D、 $x^{2} - 5 x - 13$

查看试题解析
9. 已知光速为300000千米秒，光经过t秒（ $1 \leq t \leq 10$ ）传播的距离用科学记数法表示为 $a \times 10^{n}$ 千米，则n可能为（）

A、5 B、6 C、5或6 D、5或6或7

查看试题解析
10. $\frac{2 \times 2 \times \dots \times 2}{3 + 3 + \dots + 3}$ ＝（　　），（其中m个2，n个3）

A、 $\frac{2 m}{3^{n}}$ B、 $\frac{2^{m}}{3 n}$ C、 $\frac{2 m}{n^{3}}$ D、 $\frac{m^{2}}{3 n}$

查看试题解析
11. 若a ， b互为相反数，c ， d互为倒数， $| m | = 2$ ，则 $\frac{a + b}{m^{3} + 1} + m - c d$ 的值为（）

A、4 B、－3 C、1 D、－3或1

查看试题解析
12. 下列说法错误的是（）

A、若 $a = - b$ ，则 $a^{2} = b^{2}$ B、若定义运算“*”，规定 $a * b = a (1 - b)$ 则有 $2 * (- 2) = 6$ C、若 $0 < a < 1$ ，则 $a^{2} > a^{3}$ D、若 $a > b$ ， $a b \neq 0$ ，则 $\frac{1}{a} < \frac{1}{b}$

查看试题解析
13. 如图，边长为 $(a + 3)$ 的正方形纸片，剪出一个边长为a的正方形之后，剩余部分可剪拼成一个长方形（不重叠无缝隙），若拼成长方形的一边长为3，则另一边长是（）

A、 $2 a + 3$ B、 $a + 3$ C、 $a + 6$ D、 $2 a + 6$

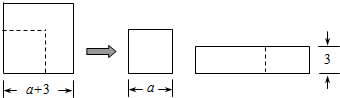查看试题解析
14. 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动：第一次将点A向左移动3个单位长度到达点A₁ ，第二次将点A向右移动6个单位长度到达点A₂ ，第三次将点A₂向左移动9个单位长度到达点A₃ ，按照这种移动规律移动下去，第n次移动到点A_n ，如果点A_n与原点的距离不小于20，那么n的最小值是（　　）

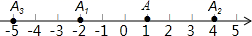A、12 B、13 C、14 D、15

查看试题解析

二、填空题

15. “m的5倍与n的差的平方”，用代数式表示为．

查看试题解析
16. 在数轴上，点A表示数－4，距A点3个单位长度的点表示的数是.

查看试题解析
17. 多项式 $- x y^{2} + \frac{x}{2} - 2 x^{3}$ 的次数是．

查看试题解析
18. 下列算式① ${(2^{2} \times 3^{2})}^{3}$ ；② $(2 \times 6^{2}) \times (3 \times 6^{3})$ ；③ $6^{3} + 6^{3}$ ；④ ${(2^{2})}^{3} \times {(3^{3})}^{2}$ 中，结果等于6 $^{6}$ 的有（填序号）．

查看试题解析

三、解答题

19. 计算

(1)、 $(- 5) + (+ 7) - (- 3) - (+ 20)$

(2)、 $25 \div \frac{5}{6} \times (- \frac{2}{5}) + (- 2) \times {(- 1)}^{2021}$

查看试题解析
20.

(1)、 $3 y^{2} - 1 - 2 y - 5 + 3 y - y^{2}$

(2)、 $3 (4 m n - m^{2}) - 4 m n - 2 (3 m n - m^{2})$

查看试题解析
21. 先化简，再求值； $3 x^{2} y - [2 x y^{2} - 2 (x y - \frac{3}{2} x^{2} y) + x y] + 3 x y^{2}$ （其中 $x = 3$ ， $y = - \frac{1}{3}$ ）

查看试题解析
22. 计算： $- 3^{2} + 2 \div \frac{2}{3} \times \frac{3}{2}$ ．
小虎同学的计算过程如下：原式 $= - 6 + 2 \div 1 = - 6 + 2 = - 4$

请你判断小虎的计算过程是否正确，若不正确，请你写出正确的计算过程．

查看试题解析
23. 老师设计了一个数学实验，给甲、乙、丙三名同学各一张写有已化为最简代数式的卡片，规则是两位同学的代数式相减等于第三位同学的代数式，则实验成功．甲、乙、丙的卡片如下，丙的卡片有一部分被遮挡了．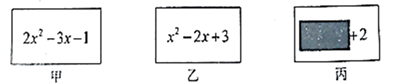

(1)、计算出甲减乙的结果，并判断甲减乙能否使实验成功；

(2)、小亮发现丙减甲可以使实验成功，请求出丙的代数式．

查看试题解析
24. 一辆货车从超市出发，向东走了 $2 km$ 到达小彬家，继续向东走了 $1.5 km$ 到达小颖家，然后向西走了 $6 km$ 到达小明家，最后回到超市．以超市为原点，向东为正方向，用一个单位长度表示 $1 km$ ，完成以下问题．

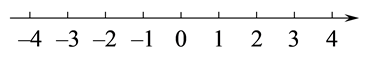(1)、以A表示小彬家，B表示小颖家，C表示小明家．在数轴上标出A、B、C的位置；

(2)、小明家距小彬家多远？

(3)、货车一共行驶了多少千米？如果货车行驶 $1 km$ 的用油量为0.35升，请你计算货车从出发到结束行程共耗油多少升？

查看试题解析
25. 阅读：已知正整数a、b、c ，显然，当同底数时，指数大的幂也大，若对于同指数，不同底数的两个幂 $a^{b}$ 和 $c^{b}$ ，当 $a > c$ 时，则有 $a^{b} > c^{b}$ ，根据上述材料，回答下列问题．

(1)、比较大小： $5^{20}$ $4^{20}$ （填写>、<或=）．

(2)、比较 $2^{33}$ 与 $3^{22}$ 的大小（写出比较的具体过程）．

(3)、计算 $4^{2021} \times {0.25}^{2020} - 8^{2021} \times {0.125}^{2020}$ ．

查看试题解析
26. 如图，从数轴上的原点开始，先向左移动2cm到达A点，再向左移动4cm到达B点，然后向右移动10cm到达C点．

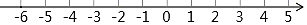(1)、用1个单位长度表示1cm，请你在题中所给的数轴上表示出A、B、C三点的位置；

(2)、把点C到点A的距离记为CA，则CA＝ ▲ cm；

(3)、若点B以每秒3cm的速度向左移动，同时A、C点以每秒lcm、5cm的速度向右移动，设移动时间为t（t＞0）秒，试探究CA﹣AB的值是否会随着t的变化而改变？请说明理由．

查看试题解析