山东省青岛市市南区2021-2022学年九年级上学期数学期中试卷

试卷更新日期：2021-11-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）

A、 $x + 2 y = 1$ B、 $x = 2 x^{3} - 3$ C、 $x^{2} - 2 = 0$ D、 $3 x + \frac{1}{x} = 1$

查看试题解析

2. 观察下列表格，一元二次方程x²﹣x＝1.1的一个解x所在的范围是（）

x	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
x²﹣x	0.11	0.24	0.39	0.56	0.75	0.96	1.19	1.44	1.71

A、1.5＜x＜1.6 B、1.6＜x＜1.7 C、1.7＜x＜1.8 D、1.8＜x＜1.9

查看试题解析

3. 某地新高考有一项“6选3”选课制，高中学生李鑫和张锋都已选了地理和生物，现在他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等，则他们恰好一人选物理，另一人选化学的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{4}$ C、 $\frac{3}{8}$ D、 $\frac{1}{2}$

查看试题解析
4. 小明同学是一位古诗文的爱好者，在学习了一元二次方程这一章后，改编了苏轼诗词《念奴娇·赤壁怀古》：“大江东去浪淘尽，千古风流人物．而立之年督东吴，早逝英年两位数．十位恰小个位三，个位平方与寿同．哪位学子算得快，多少年华数周瑜？”假设周瑜去世时年龄的十位数字是 $x$ ，则可列方程为（）

A、 $10 x + (x - 3) = {(x - 3)}^{2}$ B、 $10 (x + 3) + x = x^{2}$ C、 $10 x + (x + 3) = {(x + 3)}^{2}$ D、 $10 (x + 3) + x = {(x + 3)}^{2}$

查看试题解析
5. 已知：
问题1，某厂用2年时间把总产值增加了原来的b倍，求每年平均增长的百分数；

问题2，总产值用2年的时间在原来a万元的基础上增加了b万元，求每年平均增长的百分数；

问题3，某厂用2年的时间把总产值增加到原来的b倍，求每年平均增长的百分数．

设每年平均增长的百分数x ，那么下面的三个方程：

①（1+x）²＝b ，

②a（1+x）²＝a+b ，

③（1+x）²＝b+1，

按问题1、2、3的序号排列，相对应的是（　　）

A、①②③ B、③②① C、①③② D、②①③

查看试题解析
6. 如图，△ABC的两条高AD ， BE交于点F ，连接ED ，则下列结论：①△ADC∽△BDF；②△BEC∽△ADC；③△ABD∽△ABE；④△ABC∽△DEC；⑤△BDE∽△AED；⑥△BDF∽△AEF ．正确的为（　　）

A、①②③④ B、①②④⑥ C、①②⑤⑥ D、②③④

查看试题解析
7. 斐波那契螺旋线，也称“黄金螺旋线”，是根据斐波那契数列1，1，2，3，5，画出来的螺旋曲线．如图，白色小圆内切于边长为1的正方形，黑色曲线就是斐波那契螺旋线，它是依次在以1，2，3，5为边长的正方形中画一个圆心角为90°的扇形，将其圆弧连接起来得到的．若在矩形ABCD内随机取一点，则此点取自阴影部分的概率是（　　）

A、 $\frac{π}{4}$ B、 $\frac{39 π}{160}$ C、 $\frac{19 π + 1}{80}$ D、 $\frac{19 π + 2}{80}$

查看试题解析
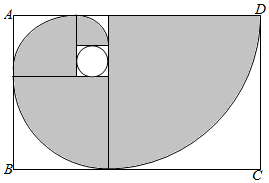8. 如图，在▱ABCD中，∠B＝60°，AB＝BC ， AE⊥BC于点E ，连接DE ，交AC于点G ．以DE为边作等边△DEF ，连接AF ，交DE于点N ，交DC于点M ，且M为AF的中点．在下列说法中：①∠EAN＝45°，② $\frac{1}{2}$ AE＝ $\sqrt{3}$ CM ， ③S_△AGE＝S_△DGC ， ④AF⊥DE ．正确的个数有（　　）

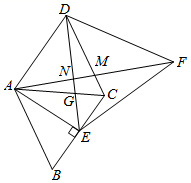A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 若 $\frac{a}{a + b} = \frac{1}{3}$ ，则 $\frac{b}{a}$ 的值为.

查看试题解析
10. 某厂一月份的产值为10万元，第一季度产值共为33.1万元，且每个月的增长率相同，若设该增长率为x ，则根据题意，可列方程：．

查看试题解析
11. 如果有12升纯酒精，倒出一部分后注满水，第二次倒出与前次同量的混合液再注满水，此时容器内的水是纯酒精的3倍，则每次倒出液体的数量是升．

查看试题解析
12. 如图，在△ABC中，D在AC边上，AD：DC＝1：2，O是BD的中点，连接AO并延长交BC于E ，则BE：EC＝．

查看试题解析
13. 如图，在矩形ABCD中，AB＝4，∠ACB＝30°，E，F分别为对角线AC与边CD上的点，且AE＝CF，则BE+BF的最小值为．

查看试题解析
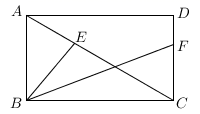14. 如图，∠MON＝45°，正方形ABB₁C ，正方形A₁B₁B₂C₁ ，正方形A₂B₂B₃C₂ ，正方形A₃B₃B₄C₃ ， …，的顶点A ， A₁ ， A₂ ， A₃ ， …，在射线OM上，顶点B ， B₁ ， B₂ ， B₃ ， B₄ ， …，在射线ON上，连接AB₂交A₁B₁于点D ，连接A₁B₃交A₂B₂于点D₁ ，连接A₂B₄交A₃B₃于点D₂ ， …，连接B₁D₁交AB₂于点E ，连接B₂D₂交A₁B₃于点E₁ ， …，按照这个规律进行下去，设△ACD与△B₁DE的面积之和为S₁ ， △A₁C₁D₁与△B₂D₁E₁的面积之和为S₂ ， △A₂C₂D₂与△B₃D₂E₂的面积之和为S₃ ， …，若AB＝2，则S_n等于．（用含有正整数n的式子表示）

查看试题解析

三、解答题

15. 请作出一个以线段a为对角线，且对角线夹角为60°的矩形ABCD ．

查看试题解析
16. 计算：请解下列方程

(1)、（y+3）（1﹣3y）＝1+2y² ．

(2)、x²+2x+2＝8x+4（配方法）

查看试题解析
17. 若关于x的一元二次方程(k﹣1)x²+2x﹣2＝0有不相等实数根，求k的取值范围.

查看试题解析
18. 某市“艺术节”期间，小明、小亮都想去观看茶艺表演，但是只有一张茶艺表演门票，他们决定采用抽卡片的办法确定谁去.规则如下：
将正面分别标有数字 1、2、3、4 的四张卡片（除数字外其余都相同）洗匀后，背面朝上放置在桌面上，随机抽出一张记下数字后放回；重新洗匀后背面朝上放置在桌面上，再随机抽出一张记下数字.如果两个数字之和为奇数，则小明去；如果两个数字之和为偶数，则小亮去.

(1)、请用列表或画树状图的方法表示抽出的两张卡片上的数字之和的所有可能出现的结果；

(2)、你认为这个规则公平吗？请说明理由.

查看试题解析
19. 已知：如图，△ABC中，D是边BC的中点，且AD＝AC ， DE⊥BC交AB于点E ， EC交AD于点F ．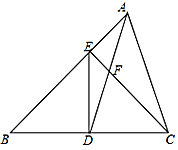

(1)、求证：△ABC∽△FCD；

(2)、求 $\frac{F C}{E F}$ 的值．

查看试题解析
20. 如图，我区荷兰花海景区东北角有一块长为60米，宽为50米的矩形荒地，地方政府准备在此扩建一个新品种花卉观光区，其中阴影部分为观览通道，通道的宽度均相等，中间的三个矩形（其中三个矩形的一边长均为a米）区域将种植新品种花卉．

(1)、设观览通道的宽度为x米，则a＝（用含x的代数式表示）；

(2)、若新品种花卉总占地面积为2430平方米．请求出观览通道的宽度为多少米？

查看试题解析
21. 如图，△ABC中，D是AB上一点，DE⊥AC于点E ， F是AD的中点，FG⊥BC于点G ，与DE交于点H ，若FG＝AF ， AG平分∠CAB ，连接GE ， GD ．

(1)、求证：△ECG≌△GHD；

(2)、当∠B为多少度时，四边形AEGF是否为菱形，请说明理由．

查看试题解析
22. 青岛某大酒店豪华间实行淡季、旺季两种价格标准，旺季每间价格比淡季上涨 $\frac{1}{3}$ .下表是去年该酒店豪华间某两天的相关记录：

淡季

旺季

未入住房间数

10

0

日总收入(元)

24000

40000

(1)、该酒店豪华间有多少间？旺季每间价格为多少元？

(2)、今年旺季来临，豪华间的间数不变，经市场调查发现，如果豪华间仍旧实行去年旺季价格，那么每天都客满：如果价格继续上涨，那么每增加25元，每天未入住房间数增加1间.不考虑其他因素，该酒店将豪华间的价格上涨多少元时，豪华间的日总收入可为42025元？

查看试题解析
23. （模型引入）
我们在全等学习中所总结的“一线三等角、K型全等”这一基本图形，可以使得我们在观察新问题的时候很迅速地联想，从而借助已有经验，迅速解决问题．

（模型探究）

如图，正方形ABCD中，E是对角线BD上一点，连接AE ，过点E作EF⊥AE ，交直线CB于点F ．

(1)、如图1，若点F在线段BC上，写出EA与EF的数量关系并加以证明；

(2)、如图2，若点F在线段CB的延长线上，请直接写出线段BC ， BE和BF的数量关系．

(3)、（模型应用）
如图3，正方形ABCD中，AB＝4，E为CD上一动点，连接AE交BD于F ，过F作FH⊥AE于F ，过H作HG⊥BD于G ．则下列结论：①AF＝FH；②∠HAE＝45°；③BD＝2FG；④△CEH的周长为8．正确的结论有个．

(4)、如图4，点E是正方形ABCD对角线BD上一点，连接AE ，过点E作EF⊥AE ，交线段BC于点F ，交线段AC于点M ，连接AF交线段BD于点H ．给出下列四个结论，①AE＝EF；② $\sqrt{2}$ DE＝CF；③S_△AEM＝S_△MCF；④BE＝DE+ $\sqrt{2}$ BF；正确的结论有个．

(5)、（模型变式）
如图5，在平面直角坐标系中，四边形OBCD是正方形，且D（0，2），点E是线段OB延长线上一点，M是线段OB上一动点（不包括点O、B），作MN⊥DM ，垂足为M ，交∠CBE的平分线与点N ，求证：MD＝MN

(6)、如图6，在上一问的条件下，连接DN交BC于点F ，连接FM ，则∠FMN和∠NMB之间有怎样的数量关系？请给出证明．

(7)、（拓展延伸）
已知∠MON＝90°，点A是射线ON上的一个定点，点B是射线OM上的一个动点，且满足OB＞OA ．点C在线段OA的延长线上，且AC＝OB ．如图7，在线段BO上截取BE ，使BE＝OA ，连接CE ．若∠OBA+∠OCE＝β ，当点B在射线OM上运动时，β的大小是否会发生变化？如果不变，请求出这个定值；如果变化，请说明理由．

(8)、如图8，正方形ABCD中，AD＝6，点E是对角线AC上一点，连接DE ，过点E作EF⊥ED ，交AB于点F ，连接DF ，交AC于点G ，将△EFG沿EF翻折，得到△EFM ，连接DM ，交EF于点N ，若点F是AB边的中点，则△EDM的面积是．

查看试题解析
24. 如图1，在矩形ABCD中，AB＝6cm，BC＝8cm，点E ， F分别为AD ， BC边的中点．动点P从点E出发沿ED向点D运动，速度为1cm/s，同时，动点Q从点F出发沿FB向点B运动，速度为2cm/s，过点Q作QM∥AC ，交AB于点M ，连接PM ， PQ ，分别交AC于点G ， H ．设运动时间为t（s）（0＜t＜2）．

(1)、连接DF ，当t为何值时，四边形PDFQ是平行四边形？

(2)、当△PQM的面积等于矩形ABCD面积的 $\frac{1}{8}$ 时，求出t的值；

(3)、是否存在某一时刻t ，使点P在线段MQ的垂直平分线上？若存在，求出t的值；若不存在，说明理由．

(4)、如图2，过点C作CN⊥PQ ，垂足为N ，连接AN ，请你求出线段AN的最小值．

查看试题解析

	淡季	旺季
未入住房间数	10	0
日总收入(元)	24000	40000