山东省济宁市嘉祥县2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-11-19 类型:期中考试
一、单选题
-
1. 在平面直角坐标系中,点 关于原点的对称点 的坐标为( )A、 B、 C、 D、2. 下列图形中,不是中心对称图形的是( )A、圆 B、菱形 C、矩形 D、等边三角形3. 为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每盒零售价由16元降为9元,设平均每次降价的百分率是x,则根据题意,下列方程正确的是( )A、16(1﹣x)2=9 B、9(1+x)2=16 C、16(1﹣2x)=9 D、9(1+2x)=164. 如图, 、 分别与 相切于 、 , , 为 上一点,则 的度数为( )
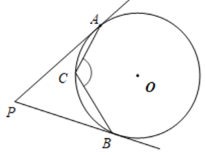 A、 B、 C、 D、5. 关于 的一元二次方程 有实数根,则 的取值范围是( )A、 且 B、 C、 且 D、6. 将抛物线 的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )A、 B、 C、 D、7. 已知(﹣3, ),(﹣2, ),(1, )是抛物线 上的点,则( )A、 B、 C、 D、8. 在 中,直径AB=15,弦DE⊥AB于点C.若OC:OB=3 :5,则DE的长为( )A、6 B、9 C、12 D、159. 在解一元二次方程x2+px+q=0时,小红看错了常数项q,得到方程的两个根是﹣3,1.小明看错了一次项系数P,得到方程的两个根是5,﹣4,则原来的方程是( )A、x2+2x﹣3=0 B、x2+2x﹣20=0 C、x2﹣2x﹣20=0 D、x2﹣2x﹣3=010. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )
A、 B、 C、 D、5. 关于 的一元二次方程 有实数根,则 的取值范围是( )A、 且 B、 C、 且 D、6. 将抛物线 的图象向右平移1个单位,再向下平移2个单位得到的抛物线必定经过( )A、 B、 C、 D、7. 已知(﹣3, ),(﹣2, ),(1, )是抛物线 上的点,则( )A、 B、 C、 D、8. 在 中,直径AB=15,弦DE⊥AB于点C.若OC:OB=3 :5,则DE的长为( )A、6 B、9 C、12 D、159. 在解一元二次方程x2+px+q=0时,小红看错了常数项q,得到方程的两个根是﹣3,1.小明看错了一次项系数P,得到方程的两个根是5,﹣4,则原来的方程是( )A、x2+2x﹣3=0 B、x2+2x﹣20=0 C、x2﹣2x﹣20=0 D、x2﹣2x﹣3=010. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )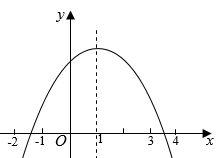 A、 个 B、 个 C、 个 D、 个
A、 个 B、 个 C、 个 D、 个二、填空题
-
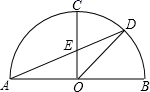
11. 抛物线 的顶点坐标为 .12. 如图, 为半圆O的直径, 平分 ,交半圆于点 交 于点E,则 的度数是 .
 13. 当﹣1≤x≤3时,二次函数y=x2﹣4x+5有最大值m,则m=.14. 如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .
13. 当﹣1≤x≤3时,二次函数y=x2﹣4x+5有最大值m,则m=.14. 如图,已知点A(2,0),B(0,4),C(2,4),D(6,6),连接AB,CD,将线段AB绕着某一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .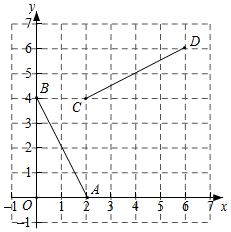 15. 如图,抛物线 与x轴只有一个公共点 ,与y轴交于点 ,虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为 .
15. 如图,抛物线 与x轴只有一个公共点 ,与y轴交于点 ,虚线为其对称轴,若将抛物线向下平移两个单位长度得抛物线 ,则图中两个阴影部分的面积和为 .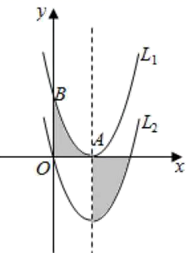
三、解答题
-
16.(1)、解方程: .(2)、解方程: .17. 如图,在平面直角坐标系中, 的三个顶点分别是A(1,3),B(4,4),C(2,1).
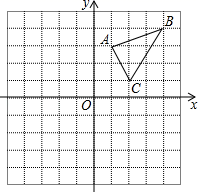
⑴把 向左平移4个单位后得到对应的 A1B1C1 , 请画出平移后的 A1B1C1;
⑵把 绕原点O旋转180°后得到对应的 A2B2C2 , 请画出旋转后的 A2B2C2;
⑶观察图形可知, A1B1C1与 A2B2C2关于点( ▲ , ▲ )中心对称.
18. 若直角三角形的两边长分别是方程 的两根,求该直角三角形的面积.19. 如图,有一张边AB靠墙的长方形桌子ABCD,长120cm,宽60 cm.有一块长方形台布EFMN的面积是桌面面积的2倍,并且如图所示铺在桌面上时,三边垂下的长度中有两边相等(AE=BF),另外一边是AE的 倍(即CD与MN之间的距离).求这块台布的长和宽. 20. 年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截而示意图,取某一位置的水平线为 轴,过跳台终点 作水平线的垂线为 轴,建立平面直角坐标系,图中的抛物线 近似表示滑雪场地上的一座小山坡,某运动员从点 正上方 米处的 点滑出,滑出后沿一段抛物线 运动.
20. 年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截而示意图,取某一位置的水平线为 轴,过跳台终点 作水平线的垂线为 轴,建立平面直角坐标系,图中的抛物线 近似表示滑雪场地上的一座小山坡,某运动员从点 正上方 米处的 点滑出,滑出后沿一段抛物线 运动.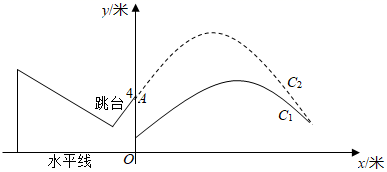 (1)、当运动员运动到离 处的水平距离为 米时,离水平线的高度为 米,求抛物线 的函数解析式(不要求写出自变量 的取值范围);(2)、在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为 米?21. 如图,以等边三角形ABC的BC边为直径画圆,交AC于点D , 于点F , 连接OF , 且 .
(1)、当运动员运动到离 处的水平距离为 米时,离水平线的高度为 米,求抛物线 的函数解析式(不要求写出自变量 的取值范围);(2)、在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为 米?21. 如图,以等边三角形ABC的BC边为直径画圆,交AC于点D , 于点F , 连接OF , 且 .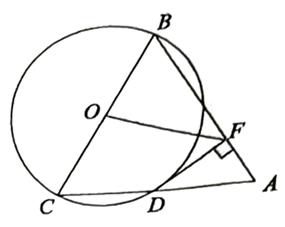 (1)、求证:DF是 的切线;(2)、求线段OF的长度.22. 如图,抛物线 与 轴相交于A,B两点,与y轴相交于点C, , ,直线l是抛物线的对称轴,在直线l右侧的抛物线上有一动点D,连接 , , , .
(1)、求证:DF是 的切线;(2)、求线段OF的长度.22. 如图,抛物线 与 轴相交于A,B两点,与y轴相交于点C, , ,直线l是抛物线的对称轴,在直线l右侧的抛物线上有一动点D,连接 , , , . (1)、求抛物线的函数表达式;(2)、若点D在x轴的下方,当 的面积是 时,求 的面积;(3)、在(2)的条件下,点M是x轴上一点,点N是抛物线上一动点,是否存在点N,使得以点B,D,M,N为顶点,以 为一边的四边形是平行四边形,若存在,求出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、若点D在x轴的下方,当 的面积是 时,求 的面积;(3)、在(2)的条件下,点M是x轴上一点,点N是抛物线上一动点,是否存在点N,使得以点B,D,M,N为顶点,以 为一边的四边形是平行四边形,若存在,求出点N的坐标;若不存在,请说明理由.