山东省东营市广饶县2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-11-19 类型:期中考试
一、单选题
-
1. 若抛物线y=﹣7(x+4)2﹣1平移得到y=﹣7x2 , 则必须( )A、先向左平移4个单位,再向下平移1个单位 B、先向右平移4个单位,再向上平移1个单位 C、先向左平移1个单位,再向下平移4个单位 D、先向右平移1个单位,再向上平移4个单位2. 在△ABC中,若|sinA﹣|+(﹣cosB)2=0,则∠C的度数是( )A、45° B、75° C、105° D、120°3. 已知 是y关于x的二次函数,则m的值为( )A、 B、 C、 或 D、4. 在同一平面直角坐标系内,二次函数 与一次函数 的图象可能是( )A、
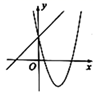 B、
B、 C、
C、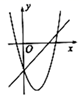 D、
D、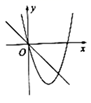 5. 如图是三个反比例函数y= ,y= ,y= 在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )
5. 如图是三个反比例函数y= ,y= ,y= 在x轴上方的图象,由此观察得到k1、k2、k3的大小关系为( )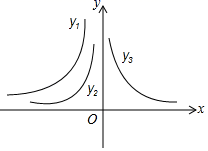 A、k1>k2>k3 B、k2>k1>k3 C、k3>k2>k1 D、k3>k1>k26. 如图,点A、B、C均在小正方形的顶点上,且每个小正方形的边长均为1,则cos∠BAC的值为( )
A、k1>k2>k3 B、k2>k1>k3 C、k3>k2>k1 D、k3>k1>k26. 如图,点A、B、C均在小正方形的顶点上,且每个小正方形的边长均为1,则cos∠BAC的值为( )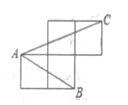 A、 B、 C、1 D、7. 已知反比例函数y= ,则( )A、y随x的增大而增大 B、当x>-3且x≠0时,y>4 C、图象位于一、三象限 D、当y<-3时,0<x<48. 如图,反比例函数y= 的图象经过▱ABCD对角线的交点P,已知点A,C,D在坐标轴上,BD⊥DC,▱ABCD的面积为6,则k的值为( )
A、 B、 C、1 D、7. 已知反比例函数y= ,则( )A、y随x的增大而增大 B、当x>-3且x≠0时,y>4 C、图象位于一、三象限 D、当y<-3时,0<x<48. 如图,反比例函数y= 的图象经过▱ABCD对角线的交点P,已知点A,C,D在坐标轴上,BD⊥DC,▱ABCD的面积为6,则k的值为( ) A、 B、 C、 D、9.
A、 B、 C、 D、9.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
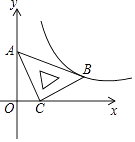 A、( ,0) B、(2,0) C、( ,0) D、(3,0)10. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示.下列结论:
A、( ,0) B、(2,0) C、( ,0) D、(3,0)10. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示.下列结论:①abc<0;②3a+c=0;
③当y>0时,x的取值范围是﹣1≤x<3;
④方程ax2+bx+c﹣3=0有两个不相等的实数根;
⑤点(﹣2,y1),(2,y2)都在抛物线上,则有y1<0<y2 .
其中结论正确的个数是( ).
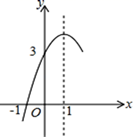 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 用配方法将二次函数y=2x2+4x+5化成 的形式是.12. 若抛物线 过原点, 则该抛物线与x轴的另一个交点坐标为 .13. 如图,抛物线 与x轴交于A、B两点,与y轴交于C点,M点在抛物线的对称轴上,当点M到点B的距离与到点C的距离之和最小时,点N的坐标为 .
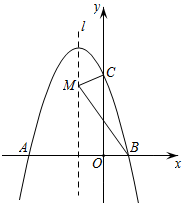 14. 某菜农搭建一个横截面为抛物线的大棚,有关尺寸如图所示,若菜农身高为 米,则他在不弯腰的情况下在大棚里横向活动的范围是米.
14. 某菜农搭建一个横截面为抛物线的大棚,有关尺寸如图所示,若菜农身高为 米,则他在不弯腰的情况下在大棚里横向活动的范围是米.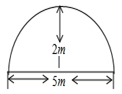 15. 若二次函数 的对称轴为直线 ,则关于 的方程 的解为.16. 已知函数y=kx2﹣2x+1的图象与x轴只有一个有交点,则k的值为.17. 在△ABC中,AB=AC,BD⊥AC于D,若cos∠BAD= ,BD= ,则CD的长为 .18. 如图,点 在反比例函数 的图象上,点 在 轴上,且 ,直线 与双曲线 交于点 , ,则 的坐标是 .
15. 若二次函数 的对称轴为直线 ,则关于 的方程 的解为.16. 已知函数y=kx2﹣2x+1的图象与x轴只有一个有交点,则k的值为.17. 在△ABC中,AB=AC,BD⊥AC于D,若cos∠BAD= ,BD= ,则CD的长为 .18. 如图,点 在反比例函数 的图象上,点 在 轴上,且 ,直线 与双曲线 交于点 , ,则 的坐标是 .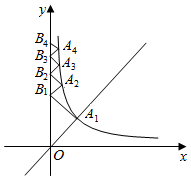
三、解答题
-
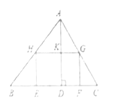
19.(1)、计算:(2)、先化简,再求代数式 的值,其中 .20. 如图三角形ABC中,有一内接矩形EFGH,AD为BC边上的高,BC=10,AD=8,矩形面积为S,AD与HG交于K,设GF为x,HG为y.
 (1)、求y与x的函数关系式,(2)、当x取何值时,S有最大值,最大值是多少?21. “武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了 条口罩生产线,每条生产线每天可生产口罩 个.如果每增加一条生产线,每条生产线就会比原来少生产 个口罩.设增加 条生产线后,每条生产线每天可生产口罩 个.(1)、直接写出 与 之间的函数关系式;(2)、若每天共生产口罩 个,在投入人力物力尽可能少的情况下,应该增加几条生产线?(3)、设该厂每天可以生产的口罩 个,请求出 与 的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?22. 如图,已知反比例函数 的图象与一次函数 的图象相交于点 和点 .
(1)、求y与x的函数关系式,(2)、当x取何值时,S有最大值,最大值是多少?21. “武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了 条口罩生产线,每条生产线每天可生产口罩 个.如果每增加一条生产线,每条生产线就会比原来少生产 个口罩.设增加 条生产线后,每条生产线每天可生产口罩 个.(1)、直接写出 与 之间的函数关系式;(2)、若每天共生产口罩 个,在投入人力物力尽可能少的情况下,应该增加几条生产线?(3)、设该厂每天可以生产的口罩 个,请求出 与 的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?22. 如图,已知反比例函数 的图象与一次函数 的图象相交于点 和点 .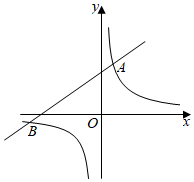 (1)、求反比例函数与一次函数的解析式;(2)、直接写出不等式 的解集;(3)、若点P是x轴上一点,且满足 的面积是 ,请求出点P的坐标.23. 2021年4月29日11时23分,中国空间站天和核心舱在海南文昌航天发射场发射升空,准确进入预定轨道,任务取得成功.建造空间站,建成国家太空实验室,是实现我国载人航天工程“三步走”战略的重要目标,是建设科技强国、航天强国的重要引领性工程.天和核心舱发射成功,标志着我国空间站建造进入全面实施阶段,为后续任务展开奠定了基础.某校航天爱好者的同学们构建数学模型,使用卷尺和测角仪测量天和核心舱的高度.如图所示,核心舱架设在1米的稳固支架上,他们先在水平地面点B处测得天和核心舱最高点A的仰角为 ,然后沿水平MN方向前进24米,到达点C处,测得点A的仰角为 ,测角仪MB的高度为1.6米,求天和核心舱的高度(结果精确到0.1米,参考数据: , , , )
(1)、求反比例函数与一次函数的解析式;(2)、直接写出不等式 的解集;(3)、若点P是x轴上一点,且满足 的面积是 ,请求出点P的坐标.23. 2021年4月29日11时23分,中国空间站天和核心舱在海南文昌航天发射场发射升空,准确进入预定轨道,任务取得成功.建造空间站,建成国家太空实验室,是实现我国载人航天工程“三步走”战略的重要目标,是建设科技强国、航天强国的重要引领性工程.天和核心舱发射成功,标志着我国空间站建造进入全面实施阶段,为后续任务展开奠定了基础.某校航天爱好者的同学们构建数学模型,使用卷尺和测角仪测量天和核心舱的高度.如图所示,核心舱架设在1米的稳固支架上,他们先在水平地面点B处测得天和核心舱最高点A的仰角为 ,然后沿水平MN方向前进24米,到达点C处,测得点A的仰角为 ,测角仪MB的高度为1.6米,求天和核心舱的高度(结果精确到0.1米,参考数据: , , , )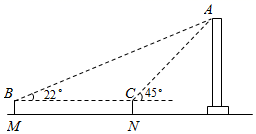 24. 泡茶需要将电热水壶中的水先烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
24. 泡茶需要将电热水壶中的水先烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.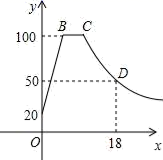 (1)、分别求出图中所对应的函数关系式,并且写出自变量x的取值范围:(2)、从水壶中的水烧开(100℃)降到90℃就可以泡茶,问从水烧开到泡茶需要等待多长时间?25. 如图①,已知抛物线 (a≠0)与 轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
(1)、分别求出图中所对应的函数关系式,并且写出自变量x的取值范围:(2)、从水壶中的水烧开(100℃)降到90℃就可以泡茶,问从水烧开到泡茶需要等待多长时间?25. 如图①,已知抛物线 (a≠0)与 轴交于点A(1,0)和点B(-3,0),与y轴交于点C. (1)、求抛物线的解析式;(2)、设抛物线的对称轴与 轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.(3)、如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
(1)、求抛物线的解析式;(2)、设抛物线的对称轴与 轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.(3)、如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.