辽宁省沈阳市于洪区2021-2022学年九年级上学期数学期中试卷
试卷更新日期：2021-11-19 类型：期中考试
一、单选题
-
1. 如图是一个“凹”字形几何体，下列关于该几何体的俯视图画法正确的是（ ）
A、
B、
C、
D、
2. a， b，c，d 是成比例线段，若 a = 3cm， b = 2cm，c = 6cm，则线段d的长为（ ）A、3cm B、4cm C、5cm D、6cm3. 将一元二次方程﹣3x2﹣2＝﹣x化成一般形式ax2＋bx＋c＝0（a＞0）后，一次项和常数项分别是（ ）A、﹣1，2 B、x ， ﹣2 C、﹣x ， 2 D、3x2 ， 24. 如图，以点O为位似中心，将△ABC放大得到△DEF，若AD＝OA，则△ABC与△DEF 的面积之比为 （ ）
A、1：2 B、1：4 C、1：5 D、1：65. 如图，点P在反比例函数y= （k≠0）的图象上，PA⊥x轴于点A，△PAO的面积为2，则k的值为（ ）
A、1 B、2 C、4 D、66. 在一个不透明的袋子里装有若干个白球和15个黄球，这些球除颜色不同外其余均相同，每次从袋子中摸出一个球记录下颜色后再放回，经过很多次重复试验，发现摸到黄球的频率稳定在0.75，则袋中白球有（ ）A、5个 B、15个 C、20个 D、35个7. 如图，在边长为3的正方形 中， ， ，则 的长是（ ）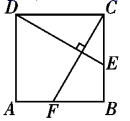
A、1 B、 C、 D、28. 目前以5G等为代表的战略性新兴产业蓬勃发展．某市2019年底有5G用户2万户，计划到2021年底全市5G用户数累计达到8.72万户，设全市5G用户数年平均增长率为x ， 根据题意可列方程是（ ）A、2（1＋x）3＝8.72 B、2（1＋x）2＝8.72 C、2（1＋x）＋2（1＋x）2＝8.72 D、2＋2（1＋x）＋2（1＋x）2＝8.729. 如图，在正方形网格中：△ABC、△EDF的顶点都在正方形网格的格点上，△ABC∽△EDF ， 则∠ABC＋∠ACB的度数为（ ）
A、75° B、60° C、55° D、45°10. 如图，有一块直角三角形余料ABC，∠BAC=90°，D是AC的中点，现从中切出一条矩形纸条DEFG，其中E，F在BC上，点G在AB上，若BF=4.5cm，CE=2cm，则纸条GD的长为（ ）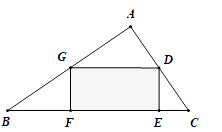
A、3 cm B、 cm C、 cm D、 cm二、填空题
-
11. 矩形的面积16，则矩形的长y与宽x（x＞0）的函数关系式 ．12. 如图，大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，P为AB的黄金分割（AP＞PB），如果AB的长度为10cm，那么PB的长度为.
13. 如图，小树AB在路灯O的照射下形成投影BC．若树高AB＝2m，树影BC＝3m，树与路灯的水平距离BP＝4m．则路灯的高度OP为m．
14. 菱形ABCD的一条对角线长为6，边AB的长是方程 的一个根，则菱形ABCD的周长为15. 若标有A，B，C的三只灯笼按图示悬挂，每次摘取一只（摘B先摘C），直到摘完，则最后一只摘到B的概率是 ．
16. 如图，在矩形ABCD中，E为C边上一点，把△ADE沿AE翻折，使点D恰好落在BC边上的点F处．若AB＝8，BC＝10，则EC＝；P ， Q分别是AE ， AD上的动点，PD＋PQ的最小值＝ ．
17. 小红家的阳台上放置了一个晒衣架，如图1，图2是晒衣架的侧面示意图，立杆AB、CD相交于点O，B、D两点在地面上，经测量得到AB=CD=136cm，OA=OC=51cm，OE=OF=34cm，现将晒衣架完全稳固张开，扣链EF成一条线段，且EF=32cm，垂挂在衣架上的连衣裙总长度小于多少时，连衣裙才不会拖在地面上？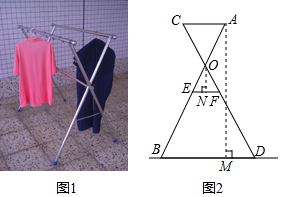
三、解答题
-
18.(1)、解方程：x2﹣4x﹣2＝0(2)、计算：若 ，且3a＋2b﹣4c＝9，求a＋b﹣c的值．19. 如图，小明与同学合作利用太阳光线测量旗杆的高度，身高1.6 m的小明落在地面上的影长为BC＝2.4 m.
(1)、请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG；(2)、若小明测得此刻旗杆落在地面的影长EG＝16 m ， 请求出旗杆DE的高度．20. 防疫期间，全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道，某天早晨，该校小明和小丽两位同学将随机通过测温通道进入校园.(1)、小明从A测温通道通过的概率是；(2)、利用画树状图或列表的方法，求小明和小丽从同一个测温通道通过的概率.21. 如图，△ABC的顶点坐标分别为A（1，3），B（4，2），C（2，1）．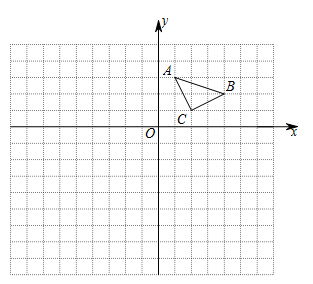
(1)、作出与△ABC关于x轴对称的△ ，点 的坐标是；(2)、以原点O为位似中心，在原点的另一侧画出△ ，使 ＝ ，点 坐标是 ．22. 如图，菱形ABCD的对角线AC、BD相交于点O ， E是AD的中点，点F、G在CD边上，EF⊥CD ， OG∥EF ．
(1)、求证：四边形OEFG是矩形；(2)、若AD＝10，EF＝4，求CG的长．23. 某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“五一”国际劳动节，商店决定采取适当的降价措施，以扩大销售量，尽快减少库存，增加利润.经市场调查发现，如果每件童装降价1元，那么平均可多售出2件.(1)、设每件童装降价 元时，每天可销售件，每件盈利元；（用 的代数式表示）(2)、为了扩大销售量，尽快减少库存，每件童装降价多少元时，平均每天赢利1200元；(3)、平均每天赢利1300元，可能吗？请说明理由.24. 某数学兴趣小组开展了一次课外活动，过程如下：如图1，正方形ABCD中，AB＝6，将三角板放在正方形ABCD上，使三角板的直角顶点与D点重合．三角板的一边交AB于点P ， 另一边交BC的延长线于点Q ．
(1)、求证：DP＝DQ；(2)、如图2，小明在图1的基础上作∠PDQ的平分线DE交BC于点E ， 连接PE ， 他发现PE和QE存在一定的数量关系，请写出结论并予以证明；(3)、如图3，固定三角板直角顶点在D点不动，转动三角板，使三角板的一边交AB的延长线于点P ， 另一边交BC的延长线于点Q ， 仍作∠PDQ的平分线DE交BC延长线于点E ， 连接PE ， 若BP＝2，请直接写出△DEP的面积．25. 如图，一次函数y＝ x＋1的图象与轴交于点A ， 与y轴交于点C ， 与反比例函数y＝ （k≠0）的图象交于B ， D两点，且AC＝BC ．
(1)、写出点A ， B的坐标；(2)、求出点D的坐标，并直接写出当 ＞ x＋1时，x的取值范围；(3)、若P是x轴上一点，PM⊥x轴交一次函数于点M ， 交反比例函数于点N ， 当O ， C ， M ， N为顶点的四边形为平行四边形时，请直接写出点P的坐标．