辽宁省锦州市北镇市2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-11-19 类型：期中考试

进入出卷网下载

一、单选题

1. 萎形不一定具备的性质是（）

A、对边平行且相等 B、对角相等 C、对角线互相平分 D、对角线相等

查看试题解析
2. 一元二次方程x²＋2x－3＝0的根的情况为（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
3. 若a、b、c、d是成比例线段，其中a=5，b=2.5，c=8，则线段d的长为（）

A、2 B、4 C、5 D、6

查看试题解析
4. 如图，在矩形ABCD中，对角线AC ， BD相交于点O ，若∠AOB＝60°，AC＝10，则图中长度为5的线段共有（）

A、2条 B、4条 C、5条 D、6条

查看试题解析
5. 如图，AB//CD//EF ，直线l₁ ， l₂与这三条平行线分别交于点A ， C ， E和点B ， D ， F ，若AC＝1，CE＝3，BD＝1.2，则BF的长为（）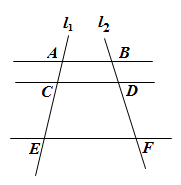

A、2.4 B、3.6 C、4.8 D、5.2

查看试题解析
6. 在一个不透明的口袋中，装有一些除颜色外完全相同的红、黑、白三种颜色的小球．已知口袋中有红球5个，白球23个，且从口袋中随机摸出一个红球的概率是 $\frac{1}{10}$ ，则口袋中黑球的个数为（）

A、22 B、23 C、25 D、27

查看试题解析
7. 如图，E ， F分别是正方形ABCD的边CD ， AD上的点，且CE＝DF ， AE与BF交于点O ，则下列结论①AE＝BF；②AE⊥BF；③O为AE中点；④S_△AOB＝S_{四边形DEOF}中，正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、多选题

8. 某农机厂4月份生产零件50万个，第二季度共生产零件182万个．设该厂5、6月份平均每月的增长率为 $x$ ，那么下列方程错误的是（）

A、 $50 {(1 + x)}^{2} = 182$ B、 $50 + 50 (1 + x) + 50 {(1 + x)}^{2} = 182$ C、 $50 (1 + 2 x) = 182$ D、 $50 + 50 (1 + x) + 50 (1 + 2 x) = 182$

查看试题解析

三、填空题

9. 如果 $\frac{a}{b} = \frac{2}{3}$ ，那么 $\frac{b - a}{a + b} =$ .

查看试题解析
10. 定义一种运算“*”，其规则为a※b＝a²﹣b² ，则方程（x+2）*5＝0的解为．

查看试题解析
11. 有三张形状、大小、质地都相同的卡片，正面分别标有数字－1，2，3，将它们背面朝上，洗匀后随机抽取一张，不放回，再随机抽取一张，则抽取的两张卡片正面标有数字都是正数的概率为

查看试题解析
12. 如图，在△ABC中，BD⊥AC于D，点E为AB的中点，AD=6，DE=5，则线段BD的长等于．

查看试题解析
13. 如图，在菱形ABCD中，∠ABC＝130°，EF垂直平分AD ，交AD于点E ，交对角线AC于点F ，连接BF ，则∠FBC的度数为

查看试题解析
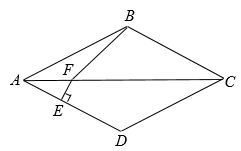14. 一个等腰三角形的两条边长分别是方程x²﹣7x+10=0的两根，则该等腰三角形的周长是．

查看试题解析
15. 如图，在矩形 $A B C D$ 中， $A B = 6$ ， $A D = 10$ ，沿过点A的直线翻折，使点D落在 $B C$ 边上的点E处，折痕与边 $C D$ 相交于点F，则 $C F$ 的长为

查看试题解析
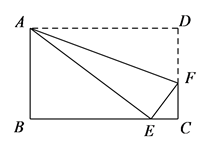16. 如图，在正方形ABCD中，E是边AB上一点，BE＝ $\sqrt{2}$ ，AE＝3BE ， P是对角线AC上一动点，连接PB ， PE ，当点P在AC上运动时，△PBE周长的最小值为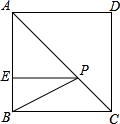

查看试题解析

四、解答题

17. 按指定的方法解方程：

(1)、x²＋2 $\sqrt{2}$ x－6＝0；（公式法）

(2)、2（x＋1）²＝x²－1（因式分解法）

查看试题解析
18. 先阅读以下材料，再按要求解答问．求代数式y²＋4y＋8的最小值．
解∶y²＋4y＋8＝y²＋4y＋4－4＋8＝y²＋4y＋4＋4＝（y＋2）²＋4，

$∵$ （y＋2）²≥0，

$∴$ （y＋2）²＋4≥4

$∴$ y²＋4y＋8的最小值是4

(1)、求代数式x²＋2x＋4的最小值；

(2)、当m为何值时，代数式m²－6m＋13有最小值，并求出这个最小值．

查看试题解析
19. 防疫期间，全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道，某天早晨，该校小明和小丽两位同学将随机通过测温通道进入校园.

(1)、小明从A测温通道通过的概率是；

(2)、利用画树状图或列表的方法，求小明和小丽从同一个测温通道通过的概率.

查看试题解析
20. 如图，在平行四边形ABCD中，点E ， G ， F分别在AD ， CD及对角线BD上，且EF//AB ， FG//BC ，若DE：DA＝2：5，EF＝4，求线段CG的长．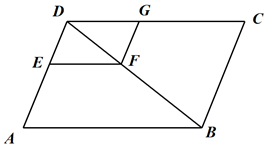

查看试题解析
21. 某服装超市购进单价为30元的童装若干件，物价部门规定其销售单价不低于每件30元，不高于每件60元．销售一段时间后发现：当销售单价为60元时，平均每月销售量为80件，而当销售单价每降低10元时，平均每月能多售出20件，同时，在销售过程中，每月还要支付其他费用450元，设销售单价为x元，平均月销售量为y件．

(1)、求出y与x的函数关系式，并写出自变量x的取值范围

(2)、当销售单价为多少元时，销售这种童装每月可获利1800元？

查看试题解析
22. 如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF⊥AB，OG∥EF．

(1)、求证：四边形OEFG是矩形；

(2)、若AD=10，EF=4，求OE和BG的长．

查看试题解析
23. 如图，在Rt△ABC中，∠C＝90°，AC＝30cm，BC－21cm，动点P从点B出发，以1cm/s的速度沿 BC方向运动，动点Q从点C出发，以同样的速度沿CA方向运动，当点P运动到点 C时，点Q随之停止运动．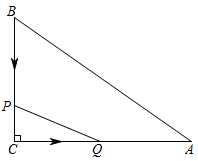

(1)、求运动多少s时，点P与点Q相距15cm；

(2)、在点P ， Q运动的过程中，△PCQ的面积能否为56cm²？请说明理由．

查看试题解析
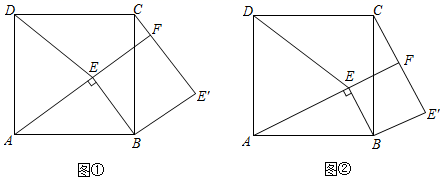
24. 问题情境：
如图1，点E为正方形ABCD内一点，∠AEB＝90°，将Rt△ABE绕点B按顺时针方向旋转90°，得到△CBE′（点A的对应点为点C）．延长AE交CE′于点F，连接DE．

猜想证明：

(1)、试判断四边形BE'FE的形状，并说明理由；

(2)、如图2，若DA＝DE，请猜想线段CF与FE'的数量关系并加以证明．

查看试题解析