黑龙江省大庆市肇源县2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-11-19 类型:期中考试
一、单选题
-
1. 在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值( )A、也扩大3倍 B、缩小为原来的 C、都不变 D、有的扩大,有的缩小2. 如图,已知Rt△ABC中,∠C=90°,AC=8,BC=15,则tanA的值为( )
 A、 B、 C、 D、3. 函数 的图象的顶点坐标是( )A、 B、 C、 D、4. 点 关于y轴对称的点的坐标是( )A、 B、 C、 D、5. 在△ABC中,若|sinA﹣ |+( ﹣cosB)2=0,∠A,∠B都是锐角,则∠C度数是( )A、75° B、90° C、105° D、120°6. 若函数 是二次函数,则m的值是( )A、2 B、-1或3 C、-1 D、37. 抛物线 的部分图象如图所示,若 ,则 的取值范围是( ).
A、 B、 C、 D、3. 函数 的图象的顶点坐标是( )A、 B、 C、 D、4. 点 关于y轴对称的点的坐标是( )A、 B、 C、 D、5. 在△ABC中,若|sinA﹣ |+( ﹣cosB)2=0,∠A,∠B都是锐角,则∠C度数是( )A、75° B、90° C、105° D、120°6. 若函数 是二次函数,则m的值是( )A、2 B、-1或3 C、-1 D、37. 抛物线 的部分图象如图所示,若 ,则 的取值范围是( ).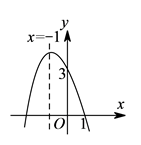 A、 B、 C、 或 D、 或8. 函数 与 在同一直角坐标系中的图象可能是( )A、
A、 B、 C、 或 D、 或8. 函数 与 在同一直角坐标系中的图象可能是( )A、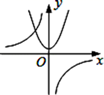 B、
B、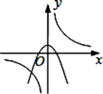 C、
C、 D、
D、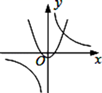 9. 在平面直角坐标系中,如果抛物线 不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( )A、 B、 C、 D、10. 已知二次函数 ,当 时,函数值为 ;当 时,函数值为 ,若 ,则下列表达式正确的是( )A、 B、 C、 D、
9. 在平面直角坐标系中,如果抛物线 不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是( )A、 B、 C、 D、10. 已知二次函数 ,当 时,函数值为 ;当 时,函数值为 ,若 ,则下列表达式正确的是( )A、 B、 C、 D、二、填空题
-
11. 试写出一个开口方向向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的解析式为.12. 若一个三角形三个内角度数的比为 ,那么这个三角形最小角的正切值为 .13. 若抛物线y=x2-2x-3与x轴分别交于A,B两点,则AB的长为 .14. 如图,在△ABC中,∠A=30°,∠B=45°,AC=2 ,则AB的长为 .
 15. 将二次函数 化成 的形式,则y= .16. 若点(2,5),(4,5)是抛物线 上的两个点,那么这条抛物线的对称轴是17. 某人沿着坡度 的山坡起点向上走了50米,则他离地面高 米.(坡度:坡面铅直高度与水平宽度的比)18. 二次函数 的部分图象如图所示,图象过点 ,对称轴为直线 ,下列结论: ; ; ; 若点 、点 、点 在该函数图象上,则 ; 若方程 的两根为 和 ,且 ,则 其中正确的结论是 .
15. 将二次函数 化成 的形式,则y= .16. 若点(2,5),(4,5)是抛物线 上的两个点,那么这条抛物线的对称轴是17. 某人沿着坡度 的山坡起点向上走了50米,则他离地面高 米.(坡度:坡面铅直高度与水平宽度的比)18. 二次函数 的部分图象如图所示,图象过点 ,对称轴为直线 ,下列结论: ; ; ; 若点 、点 、点 在该函数图象上,则 ; 若方程 的两根为 和 ,且 ,则 其中正确的结论是 .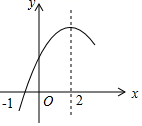
三、解答题
-
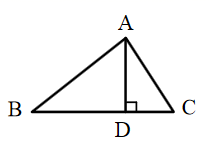
19. 计算: ;20. 如图,在 中, ,AD是BC边上的高,若 , ,求AC的长.
 21. 如图的一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是 ,求选取点B为坐标原点时的抛物线解析式.
21. 如图的一座拱桥,当水面宽AB为12 m时,桥洞顶部离水面4 m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是 ,求选取点B为坐标原点时的抛物线解析式.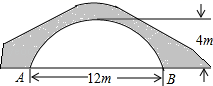 22. 一条自西向东的观光大道l上有A、B两个景点,A、B相距2km,在A处测得另一景点C位于点A的北偏东60°方向,在B处测得景点C位于景点B的北偏东45°方向,求景点C到观光大道l的距离.(答案可保留根号)
22. 一条自西向东的观光大道l上有A、B两个景点,A、B相距2km,在A处测得另一景点C位于点A的北偏东60°方向,在B处测得景点C位于景点B的北偏东45°方向,求景点C到观光大道l的距离.(答案可保留根号) 23. 已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.(1)、求k的值:(2)、若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.24. 现有一块直角三角形的材料, cm, cm,用它截下一个矩形,如图是截法示意图,求这种截法下矩形的最大面积是多少?
23. 已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.(1)、求k的值:(2)、若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.24. 现有一块直角三角形的材料, cm, cm,用它截下一个矩形,如图是截法示意图,求这种截法下矩形的最大面积是多少?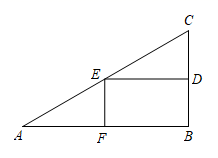 25. 根据道路管理规定,在羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M距羲皇大道l(直线)的距离MN为30米(如图所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°.
25. 根据道路管理规定,在羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M距羲皇大道l(直线)的距离MN为30米(如图所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从A点行驶到B点所用时间为6秒,∠AMN=60°,∠BMN=45°. (1)、计算AB的长度.(2)、通过计算判断此车是否超速.26. 已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)、计算AB的长度.(2)、通过计算判断此车是否超速.26. 已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.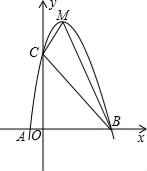 (1)、求抛物线的解析式;(2)、求△MCB的面积.27. 某商场试销一种成本为60元/件的T恤,规定试销期间单价不低于成本单价,又获利不得高于40%,经试销发现,销售量y(件)与销售单价x(元/件)符合一次函数y=kx+b , 且x=70时,y=50;x=80时,y=40;(1)、求出一次函数y=kx+b的解析式(2)、若该商场获得利润为w元,试写出利润w与销售单价x之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?28. 二次函数图象的顶点在原点O , 经过点 ;点 在y轴上.直线 与y轴交于点H .
(1)、求抛物线的解析式;(2)、求△MCB的面积.27. 某商场试销一种成本为60元/件的T恤,规定试销期间单价不低于成本单价,又获利不得高于40%,经试销发现,销售量y(件)与销售单价x(元/件)符合一次函数y=kx+b , 且x=70时,y=50;x=80时,y=40;(1)、求出一次函数y=kx+b的解析式(2)、若该商场获得利润为w元,试写出利润w与销售单价x之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?28. 二次函数图象的顶点在原点O , 经过点 ;点 在y轴上.直线 与y轴交于点H .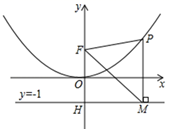 (1)、求二次函数的解析式;(2)、点P是(1)中图象上的点,过点P作x轴的垂线与直线 交于点M , 试用下图,求证:FM平分 ;
(1)、求二次函数的解析式;(2)、点P是(1)中图象上的点,过点P作x轴的垂线与直线 交于点M , 试用下图,求证:FM平分 ;