河北省唐山市路北区2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-11-19 类型:期中考试
一、单选题
-
1. 若 是一元二次方程,则有( )A、 B、a≠0 C、 D、2. 一元二次方程 的根是( )A、 , B、 , C、 , D、3. 抛物线 的顶点坐标是( )A、 B、 C、 D、4. 一元二次方程 化为一般形式是( )A、 B、 C、 D、5. 关于方程x2﹣3x﹣1=0的根的情况,下列说法正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断6. 抛物线 与y轴的交点坐标为( )A、( , ) B、( ,0) C、( , ) D、( , )7. 在平面直角坐标系中,将函数y=-x2的图像先向右平移1个单位,再向上平移5个单位后,得到的图像的函数表达式是( )A、 B、 C、 D、8. 如图是二次函数 的部分图象,则 的解的情况为( )
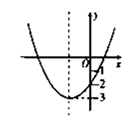 A、有唯一解 B、有两个解 C、无解 D、无法确定9. 已知函数 是常数, ,下列结论正确的是( )A、当 时,函数图象过点 B、当 时,函数图象与x轴没有交点 C、若 ,则当 时,y随x的增大而减小 D、若 ,则当 时,y随x的增大而增大10. 点A(0,y1),B(5,y2)在二次函数y=x2﹣4x+c的图象上,y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法比较11. 一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D,现测得AB=8dm,DC=2dm,则圆形标志牌的半径为( )
A、有唯一解 B、有两个解 C、无解 D、无法确定9. 已知函数 是常数, ,下列结论正确的是( )A、当 时,函数图象过点 B、当 时,函数图象与x轴没有交点 C、若 ,则当 时,y随x的增大而减小 D、若 ,则当 时,y随x的增大而增大10. 点A(0,y1),B(5,y2)在二次函数y=x2﹣4x+c的图象上,y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法比较11. 一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D,现测得AB=8dm,DC=2dm,则圆形标志牌的半径为( )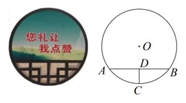 A、6dm B、5dm C、4dm D、3dm12. 在⊙O中按如下步骤作图:
A、6dm B、5dm C、4dm D、3dm12. 在⊙O中按如下步骤作图:⑴作⊙O的直径AD;
⑵以点D为圆心,DO长为半径画弧,交⊙O于B , C两点;
⑶连接DB , DC , AB , AC , BC .
根据以上作图过程及所作图形,下列四个结论中错误的是( )
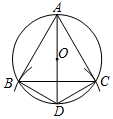 A、∠ABD=90° B、∠BAD=∠CBD C、AD⊥BC D、AC=2CD13. 如图, MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
A、∠ABD=90° B、∠BAD=∠CBD C、AD⊥BC D、AC=2CD13. 如图, MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )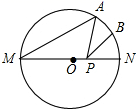 A、 B、 C、 D、14. 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于( )
A、 B、 C、 D、14. 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于( )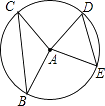 A、 B、 C、4 D、3
A、 B、 C、4 D、3二、填空题
-
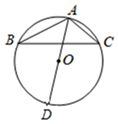
15. 若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根,则m的值为 .16. 如图, 为 的外接圆 的直径,如果 ,那么 .
 17. 如图,抛物线 与直线 相交于点 , ,则关于 的方程 的解为 .
17. 如图,抛物线 与直线 相交于点 , ,则关于 的方程 的解为 .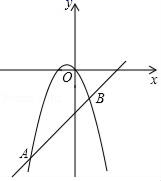 18. 已知二次函数y=﹣(x﹣a)2+a+2,当a取不同的值时,顶点在一条直线上,这条直线的解析式是 . 抛物线与y轴交点为C , 当﹣1≤a≤2时,C点经过的路径长为 .
18. 已知二次函数y=﹣(x﹣a)2+a+2,当a取不同的值时,顶点在一条直线上,这条直线的解析式是 . 抛物线与y轴交点为C , 当﹣1≤a≤2时,C点经过的路径长为 .三、解答题
-
19.(1)、 (公式法)(2)、 (因式分解法)20. 已知抛物线y=x2+bx+c的图象经过A(﹣1,12),B(0,5).(1)、求抛物线解析式;(2)、试判断该二次函数的图象是否经过点(1,2).21. 已知关于x的一元二次方程 .(1)、求证:方程总有两个实数根;(2)、若方程两个根的绝对值相等,求此时m的值.22. 张师傅今年初开了一家药店,二月份开始盈利,二月份的盈利是6000元,四月份的盈利达到8640元,且从今年二月到四月,每月盈利的平均增长率都相同.(1)、求每月盈利的平均增长率;(2)、按照这个平均增长率,预计今年五月份的盈利能达到多少元?23. 已知二次函数 .
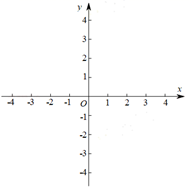 (1)、将二次函数化成 的形式;(2)、在平面直角坐标系中画出 的图象;(3)、结合函数图象,直接写出 时x的取值范围.24. 如图,AB是⊙O的直径,弦CD与AB交于点E , 且E是CD的中点.
(1)、将二次函数化成 的形式;(2)、在平面直角坐标系中画出 的图象;(3)、结合函数图象,直接写出 时x的取值范围.24. 如图,AB是⊙O的直径,弦CD与AB交于点E , 且E是CD的中点.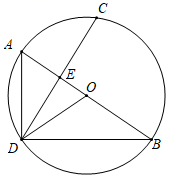 (1)、求证:∠ADC=∠BDO;(2)、若CD= ,AE=2,求⊙O的半径.25. 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)、求证:∠ADC=∠BDO;(2)、若CD= ,AE=2,求⊙O的半径.25. 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.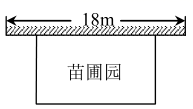 (1)、若苗圃园的面积为72平方米,求x;(2)、若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;26. 《函数的图象与性质》拓展学习片段展示:
(1)、若苗圃园的面积为72平方米,求x;(2)、若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;26. 《函数的图象与性质》拓展学习片段展示: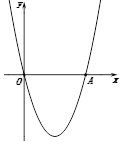
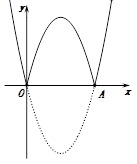

图① 图② 图③
(1)、(问题)如图①,在平面直角坐标系中,抛物线y=a(x-2)2-4经过原点O,与x轴的另一个交点为A,则a= , 点A的坐标为 .
(2)、(操作)将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方,如图②.直接写出翻折后的这部分抛物线对应的函数解析式: .
(3)、(探究)在图②中,翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象,则新图象对应的函数y随x的增大而增大时,x的取值范围是 .
(4)、(应用)结合上面的操作与探究,继续思考:如图③,若抛物线y=(x-h)2-4与x轴交于A,B两点(A在B左),将抛物线在x轴下方的部分沿x轴翻折,同样,也得到了一个“W”形状的新图象.
①求A、B两点的坐标;(用含h的式子表示)
②当1<x<2时,若新图象的函数值y随x的增大而增大,求h的取值范围.