北京市海淀区2021-2022学年九年级上学期数学期中试卷
试卷更新日期:2021-11-19 类型:期中考试
一、单选题
-
1. 方程 的二次项系数、一次项系数和常数项分别是( )A、1, , B、1,6,1 C、0, ,1 D、0,6,2. 中秋节是中国的传统节日,有“团圆”、“丰收”的寓意.月饼是首选传统食品,不仅美味,而且设计多样.下列月饼图案中,为中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 将抛物线 向下平移1个单位长度,得到的抛物线是( )A、 B、 C、 D、4. 用配方法解方程 ,下列变形正确的是( )A、 B、 C、 D、5. 如图, 是半圆O的直径,点C,D在半圆O上.若 ,则 的度数为( )
3. 将抛物线 向下平移1个单位长度,得到的抛物线是( )A、 B、 C、 D、4. 用配方法解方程 ,下列变形正确的是( )A、 B、 C、 D、5. 如图, 是半圆O的直径,点C,D在半圆O上.若 ,则 的度数为( )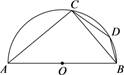 A、 B、 C、 D、6. 如图,在正三角形网格中,以某点为中心,将 旋转,得到 ,则旋转中心是( )
A、 B、 C、 D、6. 如图,在正三角形网格中,以某点为中心,将 旋转,得到 ,则旋转中心是( )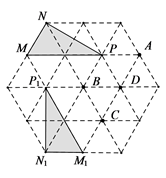 A、点A B、点B C、点C D、点D7. 已知抛物线 ,其中 , .下列说法正确的是( )A、该抛物线经过原点 B、该抛物线的对称轴在y轴左侧 C、该抛物线的顶点可能在第一象限 D、该抛物线与x轴必有公共点8. 如图,在 中, , , .动点M,N分别从A,C两点同时出发,点M从点A开始沿边 向点C以每秒1个单位长度的速度移动,点N从点C开始沿 向点B以每秒2个单位长度的速度移动.设运动时间为t,点M,C之间的距离为y, 的面积为S,则y与t,S与t满足的函数关系分别是( )
A、点A B、点B C、点C D、点D7. 已知抛物线 ,其中 , .下列说法正确的是( )A、该抛物线经过原点 B、该抛物线的对称轴在y轴左侧 C、该抛物线的顶点可能在第一象限 D、该抛物线与x轴必有公共点8. 如图,在 中, , , .动点M,N分别从A,C两点同时出发,点M从点A开始沿边 向点C以每秒1个单位长度的速度移动,点N从点C开始沿 向点B以每秒2个单位长度的速度移动.设运动时间为t,点M,C之间的距离为y, 的面积为S,则y与t,S与t满足的函数关系分别是( )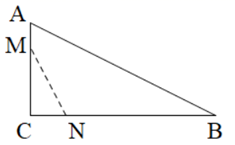 A、正比例函数关系,一次函数关系 B、正比例函数关系,二次函数关系 C、一次函数关系,正比例函数关系 D、一次函数关系,二次函数关系
A、正比例函数关系,一次函数关系 B、正比例函数关系,二次函数关系 C、一次函数关系,正比例函数关系 D、一次函数关系,二次函数关系二、填空题
-
9. 若点 与点B关于原点对称,则点B的坐标为 .10. 若点 , 都在二次函数 的图象上,则a与b的大小关系是:ab(填“>”,“<”或“=”).11. 如图,矩形 中, , .以点A为中心,将矩形 旋转得到矩形 ,使得点 落在边 上,此时 的长为 .
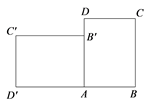 12. 如图,在平面直角坐标系 中,抛物线 的对称轴为直线 ,与x轴的一个交点为 ,则关于x的方程 的解为 .
12. 如图,在平面直角坐标系 中,抛物线 的对称轴为直线 ,与x轴的一个交点为 ,则关于x的方程 的解为 .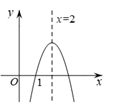 13. 如图,C , D为AB的三等分点,分别以C , D为圆心,CD长为半径画弧,两弧交于点E , F , 连接EF . 若AB=9,则EF的长为 .
13. 如图,C , D为AB的三等分点,分别以C , D为圆心,CD长为半径画弧,两弧交于点E , F , 连接EF . 若AB=9,则EF的长为 . 14. 1275年,我国南宋数学家杨辉在《田亩比类乘除算法》中提出这样一个问题:直田积八百六十四步,只云阔不及长一十二步.问阔及长各几步.意思是:矩形面积864平方步,宽比长少12步,问宽和长各几步.若设长为x步,则可列方程为.15. 数学活动课上,同学们想测出一个残损轮子的半径,小聪的解决方案如下:在轮子圆弧上任取两点A,B,连接 ,再作出 的垂直平分线,交 于点C,交 于点D,测出 , 的长度,即可计算得出轮子的半径.现测出 cm, cm,则轮子的半径为 cm.
14. 1275年,我国南宋数学家杨辉在《田亩比类乘除算法》中提出这样一个问题:直田积八百六十四步,只云阔不及长一十二步.问阔及长各几步.意思是:矩形面积864平方步,宽比长少12步,问宽和长各几步.若设长为x步,则可列方程为.15. 数学活动课上,同学们想测出一个残损轮子的半径,小聪的解决方案如下:在轮子圆弧上任取两点A,B,连接 ,再作出 的垂直平分线,交 于点C,交 于点D,测出 , 的长度,即可计算得出轮子的半径.现测出 cm, cm,则轮子的半径为 cm.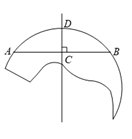 16. 已知 , 为抛物线 ( )上任意两点,其中 .若对于 ,都有 ,则a的取值范围是 .
16. 已知 , 为抛物线 ( )上任意两点,其中 .若对于 ,都有 ,则a的取值范围是 .三、解答题
-
17. 解方程: .18. 如图, 是等边三角形,点D在边 上,以 为边作等边△ .连接 , .求证: .
 19. 在平面直角坐标系 中,二次函数 的图象经过点 , .
19. 在平面直角坐标系 中,二次函数 的图象经过点 , . (1)、求这个二次函数的解析式;(2)、一次函数 ( ) 的图象也经过点A,B,结合图象,直接写出不等式 的解集.20. 如图,A,B是⊙O上的两点,C是 的中点.求证: .
(1)、求这个二次函数的解析式;(2)、一次函数 ( ) 的图象也经过点A,B,结合图象,直接写出不等式 的解集.20. 如图,A,B是⊙O上的两点,C是 的中点.求证: .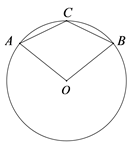 21. 已知:A,B是直线l上的两点.求作: ,使得点C在直线l上方,且 .
21. 已知:A,B是直线l上的两点.求作: ,使得点C在直线l上方,且 .
作法:
①分别以A,B为圆心, 长为半径画弧,在直线l下方交于点O;
②以点O为圆心, 长为半径画圆;
③在劣弧 上任取一点C(不与A,B重合),连接 , .
就是所求作的三角形.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:在优弧 上任取一点M(不与A,B重合),连接 , , , .
∵ ,
∴ 是等边三角形.
∴ .
∵A,B,M在⊙ 上,
∴ ()(填推理的依据).
∴ .
∵四边形 内接于⊙O,
∴ ()(填推理的依据).
∴ .
22. 已知关于x的一元二次方程 .(1)、求证:该方程总有两个不相等的实数根;(2)、若该方程的两个根均为负数,求a的取值范围.23. 小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为x轴方向,1m为单位长度,建立了如图所示的平面直角坐标系,铅球从y轴上的A点出手,运动路径可看作抛物线,在B点处达到最高位置,落在x轴上的点C处.小明某次试投时的数据如图所示.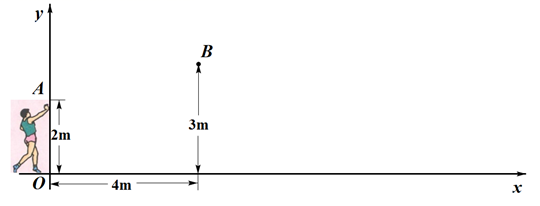 (1)、在图中画出铅球运动路径的示意图;(2)、根据图中信息,求出铅球路径所在抛物线的表达式;(3)、若铅球投掷距离(铅球落地点C与出手点A的水平距离 的长度)不小于10m,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.24. 关于x的一元二次方程 经过适当变形,可以写成 ( ) 的形式.现列表探究 的变形:
(1)、在图中画出铅球运动路径的示意图;(2)、根据图中信息,求出铅球路径所在抛物线的表达式;(3)、若铅球投掷距离(铅球落地点C与出手点A的水平距离 的长度)不小于10m,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.24. 关于x的一元二次方程 经过适当变形,可以写成 ( ) 的形式.现列表探究 的变形:变形
m
n
p
5
0
4
3
1
t
6
2
2
7
回答下列问题:
(1)、表格中t的值为;(2)、观察上述探究过程,表格中m与n满足的等量关系为;(3)、记 的两个变形为 和 ( ),则 的值为 .25. 如图, 为⊙O的直径,弦 与 交于点E, , . (1)、求 的度数;(2)、若 ,求 的长.26. 在平面直角坐标系 中,抛物线 ( )经过点 ,与y轴交于点B.(1)、直接写出点B的坐标;(2)、点 是抛物线上一点,当点P在抛物线上运动时,n存在最大值N.
(1)、求 的度数;(2)、若 ,求 的长.26. 在平面直角坐标系 中,抛物线 ( )经过点 ,与y轴交于点B.(1)、直接写出点B的坐标;(2)、点 是抛物线上一点,当点P在抛物线上运动时,n存在最大值N.①若 ,求抛物线的表达式;
②若 ,结合函数图象,直接写出N的取值范围.
27. 如图,已知 ( ), 是 的平分线,A,B分别在 , 上,且 ∥ .以点A为中心,将线段 旋转到 处,使点O的对应点C恰好在射线 上,在射线 上取一点D,使得 .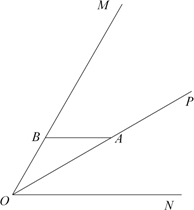 (1)、①依题意补全图;
(1)、①依题意补全图;②求证: = + ;
(2)、连接 ,若 ,求α 的度数,并直接写出 的值.28. 在平面直角坐标系xOy中,对于第一象限的P , Q两点,给出如下定义:若y轴正半轴上存在点 , 轴正半轴上存在点 ,使 ,且 (如图1),则称点P与点Q为 -关联点.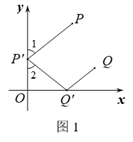 (1)、在点 , 中,与 为45°-关联点的是;(2)、如图2, , , .若线段 上存在点Q,使点P与点Q为45°-关联点,结合图象,求m的取值范围;
(1)、在点 , 中,与 为45°-关联点的是;(2)、如图2, , , .若线段 上存在点Q,使点P与点Q为45°-关联点,结合图象,求m的取值范围;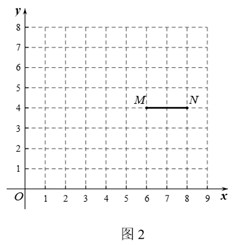 (3)、已知点 , .若线段 上至少存在一对30°-关联点,直接写出n的取值范围.
(3)、已知点 , .若线段 上至少存在一对30°-关联点,直接写出n的取值范围.