山东省青岛市市南区2021-2022学年八年级上学期数学期中试卷
试卷更新日期:2021-11-19 类型:期中考试
一、单选题
-
1. 在下列四组数中,属于勾股数的是( )A、0.3,0.4,0.5 B、9,40,41 C、2,8,10 D、1, ,2. 在二次根式 , , , , , , 中,最简二次根式的个数为( )A、1个 B、2个 C、3个 D、4个3. 已知 , ,且 ,则 的值为( )A、2或12 B、2或 C、 或12 D、 或4. 如图,象棋盘上“将”位于点 ,“象”位于点 ,则“炮”位于点
 A、 B、 C、 D、5. 实数a、b在数轴上的位置如图所示,那么化简 +|b|的结果是( )
A、 B、 C、 D、5. 实数a、b在数轴上的位置如图所示,那么化简 +|b|的结果是( ) A、a﹣2b B、﹣a C、a D、﹣2a+b6. 若等腰三角形的周长是80cm,则能反映这个等腰三角形的腰长y(cm)与底边长x(cm)的函数关系的图像是( )A、
A、a﹣2b B、﹣a C、a D、﹣2a+b6. 若等腰三角形的周长是80cm,则能反映这个等腰三角形的腰长y(cm)与底边长x(cm)的函数关系的图像是( )A、 B、
B、 C、
C、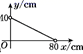 D、
D、 7. 如图,在平面直角坐标系上有个点P(1,0),点P第一次向上跳运1个单位至P1(1,1),紧接着第二次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是( )
7. 如图,在平面直角坐标系上有个点P(1,0),点P第一次向上跳运1个单位至P1(1,1),紧接着第二次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是( ) A、(-24,49) B、(-25,50) C、(26,50) D、(26,51)8. 在同一直角坐标系中,一次函数y=kx+b和y=bx+k的图象可能正确的是( )A、
A、(-24,49) B、(-25,50) C、(26,50) D、(26,51)8. 在同一直角坐标系中,一次函数y=kx+b和y=bx+k的图象可能正确的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 点P(4,0)到点Q(5,﹣12)的距离是 .10. 在平面直角坐标系xOy中,点A(﹣4,0),B(2,0)在x轴上,若点P到两坐标轴的距离相等,且∠APO=∠BPO , 则点P的坐标为 .11. 八个边长为 的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为 .
 12. 如图,∠BAC=∠DAF=90°,AB=AC , AD=AF , AB和FE交于点M , 点D , E为BC边上的两点,且∠DAE=45°,连接EF , BF , 则下列结论:①△AFB≌△ADC;②BE2+DC2=DE2;③AB﹣AD=ED﹣BE;④只有当∠AME=90°时,BF=BE , 其中正确的有 .
12. 如图,∠BAC=∠DAF=90°,AB=AC , AD=AF , AB和FE交于点M , 点D , E为BC边上的两点,且∠DAE=45°,连接EF , BF , 则下列结论:①△AFB≌△ADC;②BE2+DC2=DE2;③AB﹣AD=ED﹣BE;④只有当∠AME=90°时,BF=BE , 其中正确的有 . 13. 已知A、B、C三地顺次在同一直线上,A、C两地相距1400千米,甲乙两车均从A地出发,向B地方向匀速前进,甲车出发5小时后,乙车出发,经过一段时间后两车在B地相遇,甲车到达B地后便在B地卸货,卸完货后从B地按原车速的 返回A地,而乙车到B地后立刻继续以原速前往C地,到达C地后按原车速的 原路返回A地,结果甲乙两车同时返回A地,若两车间的距离y(千米)与甲车出发时间x(小时)之间的关系如图所示,则甲车在B地卸货用了小时.
13. 已知A、B、C三地顺次在同一直线上,A、C两地相距1400千米,甲乙两车均从A地出发,向B地方向匀速前进,甲车出发5小时后,乙车出发,经过一段时间后两车在B地相遇,甲车到达B地后便在B地卸货,卸完货后从B地按原车速的 返回A地,而乙车到B地后立刻继续以原速前往C地,到达C地后按原车速的 原路返回A地,结果甲乙两车同时返回A地,若两车间的距离y(千米)与甲车出发时间x(小时)之间的关系如图所示,则甲车在B地卸货用了小时. 14. 如图所示的正方体木块的棱长为3cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②所示的几何体,一只蚂蚁沿着图②中的几何体表面从顶点A爬行到顶点B的最短距离为cm.
14. 如图所示的正方体木块的棱长为3cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②所示的几何体,一只蚂蚁沿着图②中的几何体表面从顶点A爬行到顶点B的最短距离为cm.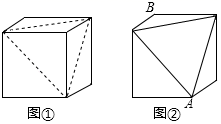
三、解答题
-
15. 完成二次根式的化简:(1)、 × × ;(2)、 +| ﹣ |+ (2﹣ )× ;(3)、 × + × +(﹣2 )﹣1;(4)、 ;(5)、| |× ;(6)、 ×(﹣ )﹣ + × .16. 作图
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:

⑴在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
⑵在第二象限内的格点上画一点C , 使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数;
⑶△ABC的周长= ▲ (结果保留根号);
⑷画出△ABC关于y轴对称的△A′B′C′.
17. 在下列 网格中分别画出一个符合条件的直角三角形,要求三角形的顶点均在格点上,且满足: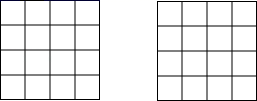 (1)、三边均为有理数;(2)、其中只有一边为无理数.18. 如图,在△ABC中,AD⊥BC , AD=12,BD=16,CD=5,求:
(1)、三边均为有理数;(2)、其中只有一边为无理数.18. 如图,在△ABC中,AD⊥BC , AD=12,BD=16,CD=5,求: (1)、△ABC的周长;(2)、△ABC是否是直角三角形?为什么?19. 随着春节临近,某儿童游乐场推出了甲、乙两种消费卡,设消费次数为x时,所需费用为y元,且y与x的函数关系如图所示. 根据图中信息,解答下列问题;
(1)、△ABC的周长;(2)、△ABC是否是直角三角形?为什么?19. 随着春节临近,某儿童游乐场推出了甲、乙两种消费卡,设消费次数为x时,所需费用为y元,且y与x的函数关系如图所示. 根据图中信息,解答下列问题;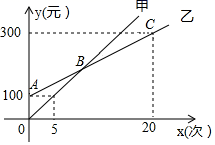 (1)、分别求出选择这两种卡消费时,y关于x的函数表达式.(2)、求出B点坐标.(3)、洋洋爸爸准备 元钱用于洋洋在该游乐场消费,请问选择哪种消费卡划算?20. 如图所示,一架梯子AB斜靠在墙面上,且AB的长为2.5米.
(1)、分别求出选择这两种卡消费时,y关于x的函数表达式.(2)、求出B点坐标.(3)、洋洋爸爸准备 元钱用于洋洋在该游乐场消费,请问选择哪种消费卡划算?20. 如图所示,一架梯子AB斜靠在墙面上,且AB的长为2.5米. (1)、若梯子底端离墙角的距离OB为1.5米,求这个梯子的顶端A距地面有多高?(2)、在(1)的条件下,如果梯子的顶端A下滑0.5米到点A',那么梯子的底端B在水平方向滑动的距离BB'为多少米?21. 甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)、若梯子底端离墙角的距离OB为1.5米,求这个梯子的顶端A距地面有多高?(2)、在(1)的条件下,如果梯子的顶端A下滑0.5米到点A',那么梯子的底端B在水平方向滑动的距离BB'为多少米?21. 甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: (1)、甲登山上升的速度是每分钟米,乙在A地时距地面的高度b为米;(2)、若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.(3)、登山多长时间时,甲、乙两人距地面的高度差为50米?22. (定义)我们定义一种三角形,两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.(1)、(感知)若△ABC三边长分别是2,2 和 ,判断此三角形是否奇异三角形,说明理由;(2)、(思考)已知Rt△ABC中,两边长分别是5,5 ,若这个三角形是奇异三角形,则第三边长是;(3)、(运用)若Rt△ABC是奇异三角形,直角边为a、b(a<b),斜边为c,求a:b:c的值.(比值从小到大排列)(4)、(创新)如图,以AB为斜边分别在AB的两侧作直角三角形,且AD=BD,若四边形ADBC内存在点E,使得AE=AD,CB=CE.试说明:△ACE是奇异三角形.
(1)、甲登山上升的速度是每分钟米,乙在A地时距地面的高度b为米;(2)、若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.(3)、登山多长时间时,甲、乙两人距地面的高度差为50米?22. (定义)我们定义一种三角形,两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.(1)、(感知)若△ABC三边长分别是2,2 和 ,判断此三角形是否奇异三角形,说明理由;(2)、(思考)已知Rt△ABC中,两边长分别是5,5 ,若这个三角形是奇异三角形,则第三边长是;(3)、(运用)若Rt△ABC是奇异三角形,直角边为a、b(a<b),斜边为c,求a:b:c的值.(比值从小到大排列)(4)、(创新)如图,以AB为斜边分别在AB的两侧作直角三角形,且AD=BD,若四边形ADBC内存在点E,使得AE=AD,CB=CE.试说明:△ACE是奇异三角形. 23. 提出问题:已知平面直角坐标系内,任意一点A , 到另外一个点B之间的距离是度多少?
23. 提出问题:已知平面直角坐标系内,任意一点A , 到另外一个点B之间的距离是度多少? (1)、问题解决:
(1)、问题解决:
遇到这种问题,我们可以先从特例入手,最后推理得出结论探究一:点A(1,﹣1)到B(﹣1,﹣1)的距离d1= ,
探究二:点A(2,﹣2)到B(﹣1,﹣1)的距离d1= ,
一般规律:
如图1,在平面直角坐标系xOy内已知A(x1 , y1)、B(x2 , y2),我们可以表示连接AB , 在构造直角三角形,使两条边交于M , 且∠M=90°,此时AM= , BM= , AB= .
(2)、已知互相平行的直线y=x﹣2与y=x+b之间的距离是3 ,试求b的值.拓展延伸:
拓展一:已知点M(﹣1,3)与直线y=2x上一点N的距离是3,则△OMN的面积是 .
拓展二:如图2,已知直线y= 分别交x , y轴于A , B两点,⊙C是以C(2,2)为圆心,2为半径的圆,P为⊙C上的动点,试求△PAB面积的最大值 .
24. 如图,在平面直角坐标系中,直线y=2x+6与x轴交于点A,与y轴交于点B,过点B的直线交x轴于点C,且AB=BC. (1)、求直线BC的解析式;(2)、点P为线段AB上一点,点Q为线段BC延长线上一点,且AP=CQ,设点Q横坐标为m,求点P的坐标(用含m的式子表示,不要求写出自变量m的取值范围);(3)、在(2)的条件下,点M在y轴负半轴上,且MP=MQ,若∠BQM=45°,求直线PQ的解析式.
(1)、求直线BC的解析式;(2)、点P为线段AB上一点,点Q为线段BC延长线上一点,且AP=CQ,设点Q横坐标为m,求点P的坐标(用含m的式子表示,不要求写出自变量m的取值范围);(3)、在(2)的条件下,点M在y轴负半轴上,且MP=MQ,若∠BQM=45°,求直线PQ的解析式.