山东省济南市历城区2021-2022学年八年级上学期数学期中试卷
试卷更新日期:2021-11-19 类型:期中考试
一、单选题
-
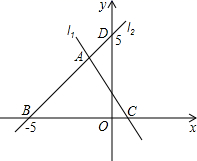
1. 下列四个数中,无理数是( )A、 B、0 C、0.12 D、π2. 的算术平方根为( )A、 B、- C、± D、3. 点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 在平面直角坐标系xOy中,点A(-2,4)关于x轴对称的点B的坐标是( )A、(-2,4) B、(-2,-4) C、(2,-4) D、(2,4)5. 下列计算正确的是( )A、 B、 C、 D、6. 在①y=-8x , ②y= ,③y=x+1,④y=-5x2+1,⑤y=0.5x-3中,一次函数有( )A、1个 B、2个 C、3个 D、4个7. 下列方程组为二元一次方程组的是( )A、 B、 C、 D、8. 点P在四象限,且点P到x轴的距离为4,点P到y轴的距离为5,则点P的坐标为( )A、(-4,-5) B、(4,-5) C、(5,4) D、(5,-4)9. 若函数y=(m-1) +3是一次函数,则m的值为( )A、-1 B、1 C、0 D、-1或110. 已知 是二元一次方程组 的解,则﹣ab的值为( )A、﹣9 B、9 C、﹣8 D、811. 若一次函数y=kx+b的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )A、
 B、
B、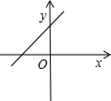 C、
C、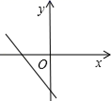 D、
D、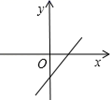 12. 正方形A1B1C1O、A2B2C2C1、A3B3C3C2 . ..按如图所示放置,点A1 , A2 , A3和点C1 , C2 , C3 . ..,分别在直线y=kx+b(k>0)和x轴上,已知点B1 , B2 , B3 , B4的坐标分别为(1,1),(3,2),(7,4),(15,8),则Bn的坐标是( )
12. 正方形A1B1C1O、A2B2C2C1、A3B3C3C2 . ..按如图所示放置,点A1 , A2 , A3和点C1 , C2 , C3 . ..,分别在直线y=kx+b(k>0)和x轴上,已知点B1 , B2 , B3 , B4的坐标分别为(1,1),(3,2),(7,4),(15,8),则Bn的坐标是( )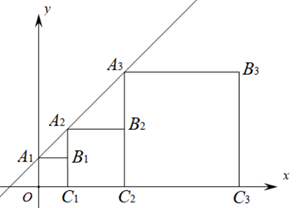 A、(2n-1,2n-1) B、(2n , 2n-1) C、(2n-1 , 2n) D、(2n-1 , 2n-1)
A、(2n-1,2n-1) B、(2n , 2n-1) C、(2n-1 , 2n) D、(2n-1 , 2n-1)二、填空题
-
13. 计算 =;14. 在平面直角坐标系中,点 在y轴上,则a的值是 .15. 若一次函数y=3x+1的图象经过点(2,m),则m=;16. 已知 , 满足方程组 ,则x+y= .17. 一次函数y= -2x+4的图象与坐标轴所围成的三角形面积是 .18. 甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差S(米)与甲出发时间t(分)之间的函数关系如图所示.下列说法:①乙先到达科技馆;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中,正确的是 (填序号).

三、解答题
-
19. 计算:(1)、 ;(2)、 ;(3)、 ;(4)、 .20. 解方程组(1)、(2)、21. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
 (1)、在图中作出 关于y轴对称的 .(2)、写出点 的坐标(直接写答案).(3)、 的面积为22. 阅读理解.
(1)、在图中作出 关于y轴对称的 .(2)、写出点 的坐标(直接写答案).(3)、 的面积为22. 阅读理解.∵ < < ,即2< <3.
∴1< ﹣1<2
∴ ﹣1的整数部分为1,
∴ ﹣1的小数部分为 ﹣2.
解决问题:已知a是 ﹣3的整数部分,b是 ﹣3的小数部分.
(1)、求a,b的值;(2)、求(﹣a)3+(b+4)2的平方根,提示:( )2=17.23. 小锦和小丽购买了价格分别相同的中性笔和笔芯.小锦买了20支笔和2盒笔芯,用了56元;小丽买了2支笔和3盒笔芯,仅用了28元.求每支中性笔和每盒笔芯的价格.24. 小明一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L , 行驶,若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系,如图所示,根据图象回答下列问题; (1)、小汽车行驶小时后加油,中途加油升;(2)、求加油前邮箱余油量Q与行驶时间t的函数关系式;(3)、如果小汽车在行驶过程中耗油量速度不变,加油站距景点300km , 车速为80km/h , 要到达目的地,油箱中的油是否够用?请说明理由.25. 已知直线y=(2m+4)x+m-3,求(1)、当m时,y随x的增大而增大;(2)、当m时,函数图象与y轴的交点在x轴下方;(3)、当m时,函数图象经过原点;(4)、当m时,这条直线平行于直线y=-x .
(1)、小汽车行驶小时后加油,中途加油升;(2)、求加油前邮箱余油量Q与行驶时间t的函数关系式;(3)、如果小汽车在行驶过程中耗油量速度不变,加油站距景点300km , 车速为80km/h , 要到达目的地,油箱中的油是否够用?请说明理由.25. 已知直线y=(2m+4)x+m-3,求(1)、当m时,y随x的增大而增大;(2)、当m时,函数图象与y轴的交点在x轴下方;(3)、当m时,函数图象经过原点;(4)、当m时,这条直线平行于直线y=-x .