辽宁省沈阳市区域业务联合体2021-2022学年八年级上学期数学期中试卷

试卷更新日期：2021-11-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四组数中，是勾股数的是（）

A、0.3，0.4，0.5 B、 $3^{2}$ ， $4^{2}$ ， $5^{2}$ C、 $\frac{1}{3}$ ， $\frac{1}{4}$ ， $\frac{1}{5}$ D、30，40，50

查看试题解析
2. 在实数 $\frac{22}{7}$ ， $\sqrt{7}$ ， $\frac{π}{3}$ ， $0.1010010001$ ， $\sqrt{36}$ ， $\sqrt[3]{2}$ 中，无理数有（）

A、1 B、2 C、3 D、4

查看试题解析
3. 在平面直角坐标系中，点（1，5）所在的象限是（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 估算 $\sqrt{24}$ ＋3的值（）

A、在5和6之间 B、在6和7之间 C、在7和8之间 D、在8和9之间

查看试题解析
5. 如图，在 $△ A B C$ 中，有一点P在 $B C$ 边上移动，若 $A B = A C = 5$ ， $B C = 6$ ，则 $A P$ 的最小值为（）

A、4.8 B、5 C、4 D、3

查看试题解析
6. 有一个数值转换器，原理如下，当输入的x为81时，输出的y是（）

A、 $\sqrt{3}$ B、9 C、3 D、 $2 \sqrt{3}$

查看试题解析
7. 在平面直角坐标系中，点A的坐标为（-4，3），AB∥y轴，AB=5，则点B的坐标为（）

A、（1，3） B、（-4，8） C、（-4，8）或（-4，-2） D、（1，3）或（-9，3）

查看试题解析
8. 如图，用4个相同的直角三角形与一个小正方形拼成的大正方形，若图中直角三角形较短的直角边长是5，小正方形的边长是7，则大正方形的面积是（）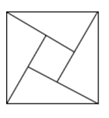

A、121 B、144 C、169 D、196

查看试题解析
9. 如图，长方形 $O A B C$ 的边 $O A$ 长为2，边 $A B$ 长为1， $O A$ 在数轴上，以原点O为圆心，对角线 $O B$ 的长为半径画弧，交正半轴于一点，则这个点表示的实数是（）

A、 $\sqrt{3}$ B、 $2 \sqrt{2}$ C、 $\sqrt{5}$ D、2.5

查看试题解析
10. 有一个面积为1的正方形，经过一次“生长”后，在它的左右肩上生出两个小正方形（如图①），其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，生出了4个正方形（如图②），如果按此规律继续“生长”下去，那么它将变得“枝繁叶茂”．在“生长”了2021次后形成的图形中所有正方形的面积和是（）

A、2019 B、2020 C、2021 D、2022

查看试题解析

二、填空题

11. $\frac{1}{16}$ 的算术平方根为．

查看试题解析
12. 已知一个直角三角形的两条边长分别是2和4，则斜边的长是．

查看试题解析
13. 已知点P（3，a）关于y轴的对称点为Q（b，2），则ab= ．

查看试题解析
14. 如图，在三角形纸片 $A B C$ 中， $∠ C = 90 °$ ， $A C = 18$ ，将 $∠ A$ 沿 $D E$ 折叠，使点A与点B重合，折痕和 $A C$ 交于点E， $E C = 5$ ，则 $B C$ 的长为．

查看试题解析
15. 如图，在平面直角坐标系中，点B的坐标为 $(3 ， 1)$ ， $A B = O B$ ， $∠ A B O = 90 °$ ，则点A的坐标是．

查看试题解析
16. 如图，在直角坐标系上有两点 $A (- 3 ， 0)$ 、 $B (0 ， 4)$ ，M是y轴上一点，若将 $△ A B M$ 沿 $A M$ 折叠，点B恰好落在x轴上，则点M的坐标为．

查看试题解析

三、解答题

17. 计算： $\frac{\sqrt{27} - \sqrt{12}}{\sqrt{3}} + (\sqrt{2} - 1) (\sqrt{2} + 1)$

查看试题解析
18. 计算： $(\sqrt{5} + 1) (\sqrt{5} - 1) - {(- \frac{1}{3})}^{- 2} + \frac{\sqrt{45}}{\sqrt{5}} + \sqrt{8}$ ．

查看试题解析
19. 如图，在四边形ABCD中，AB＝BC＝2，CD=3，DA＝1，且AB⊥BC于B ．

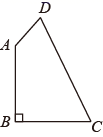
求：

(1)、∠BAD的度数；

(2)、四边形ABCD的面积．

查看试题解析
20. 已知 $x = 1 - 2 a ， y = 3 a - 4$ .

(1)、已知x的算数平方根为3，求a的值；

(2)、如果x，y都是同一个数的平方根，求这个数．

查看试题解析
21. 如图所示，在平面直角坐标系中 $△ A B C$ 的三个顶点坐标分别为 $A (- 2 ， 4)$ ， $B (- 4 ， 2)$ ， $C (- 3 ， 1)$ ．

(1)、作出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、 $△ A B C$ 的面积为， $A C$ 边上的高为；

(3)、在y轴找一点P，使得 $△ A B P$ 的周长最小，请画出点P，并直接写出 $△ A B P$ 的周长最小值为；

(4)、在x轴上找一点P，使得 $△ A B P$ 为等腰三角形，则点P的坐标为．

查看试题解析
22. 观察下列一组式的变形过程，然后回答问题：
化简： $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{{(\sqrt{2})}^{2} - 1} = \frac{\sqrt{2} - 1}{1} = \sqrt{2} - 1$ ，

则 $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}} = \sqrt{4} - \sqrt{3}$ ， $\frac{1}{\sqrt{5} + \sqrt{4}} = \sqrt{5} - \sqrt{4} \dots$

(1)、请直接写出下列式子的值： $\frac{1}{\sqrt{6} + \sqrt{5}} =$ ； $\frac{1}{\sqrt{100} + \sqrt{99}} =$ ．

(2)、请利用材料给出的结论，计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{100} + \sqrt{99}}$ 的值；

(3)、请利用材料提供的方法，计算 $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + \dots + \frac{1}{\sqrt{101} + \sqrt{99}}$ 的值．

查看试题解析
23. 在等腰 $R t △ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ．

(1)、如图1，D，E是等腰 $R t △ A B C$ 斜边 $B C$ 上两动点，且 $∠ D A E = 45 °$ ，在等腰 $R t △ A B C$ 外侧作 $△ C A F ≅ △ B A E$ ，连接 $D F$ ．
问：① $∠ D C F =$ 度．

② $△ A E D$ 与 $△ A F D$ 是否全等？请说明理由；

③当 $B E = 3$ ， $C E = 7$ 时，求 $D E$ 的长；

(2)、如图2，点D是等腰 $R t △ A B C$ 斜边 $B C$ 所在射线 $C B$ 上的一动点，连接 $A D$ ，以点A为直角顶点作等腰 $R t △ A D E$ （点E在点D的顺时针方向上），当 $B D = 4$ ， $B C = 12$ 时，直接可出 $D E$ 的长．

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，点 $A (a ， 0)$ ， $B (c ， c)$ ， $C (0 ， c)$ ，且满足 ${(a + 8)}^{2} + \sqrt{c + 4} = 0$ ， P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动，Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动．

(1)、直接写出点B的坐标， $A O$ 和 $B C$ 位置关系是；

(2)、如图（1）当P、Q分别在线段 $A O$ ， $O C$ 上时，连接 $P B$ ， $Q B$ ，使 $S_{△ P A B} = 2 S_{△ Q B C}$ ，请直接写出点P的坐标；

(3)、在P、Q的运动过程中，当 $∠ C B Q = 30 °$ 时，请直接写出 $∠ O P Q$ 和 $∠ P Q B$ 的数量关系；

(4)、当 $△ P O Q$ 为等腰直角三角形时，请直接写出 $t$ 值．

查看试题解析