江西省萍乡市湘东区2020-2021学年八年级下学期数学期中试卷

试卷更新日期：2021-11-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的有（）

A、 B、 C、 D、

查看试题解析
2. 如果不等式组 ${\begin{array}{l} x > 5 \\ x > a \end{array}$ 的解集是 $x > 5$ ，则a的取值范围是（）

A、 $a \geq 5$ B、 $a \leq 5$ C、 $a = 5$ D、 $a < 5$

查看试题解析
3. 如图，在△ABC中，∠A为钝角，AB=20cm，AC=12cm，点P从点B出发以3cm/s的速度向点A运动，点Q同时从点A出发以2cm/s的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动.当△APQ是等腰三角形时，运动的时间是（）

A、2.5s B、3s C、3.5s D、4s

查看试题解析
4. 在平面直角坐标系中，将点A（1，﹣2）向上平移3个单位长度，再向左平移2个单位长度，得到点A′，则点A′的坐标是（）

A、（﹣1，1） B、（﹣1，﹣2） C、（﹣1，2） D、（1，2）

查看试题解析
5. 下列不等式变形错误的是（）

A、若 a＞b，则 1﹣a＜1﹣b B、若 a＜b，则 ax²≤bx² C、若 ac＞bc，则 a＞b D、若 m＞n，则 $\frac{m}{x^{2} + 1}$ ＞ $\frac{n}{x^{2} + 1}$

查看试题解析
6. 如图，在直角坐标系中，已知点A（﹣3，0）、B（0，4），对△OAB连续作旋转变换，依次得到△₁、△₂、△₃、△₄、…，△₁₆的直角顶点的坐标为（）

A、（60，0） B、（72，0） C、（67 $\frac{1}{5}$ ， $\frac{9}{5}$ ） D、（79 $\frac{1}{5}$ ， $\frac{9}{5}$ ）

查看试题解析

二、填空题

7. 不等式4-x＞1的正整数解为．

查看试题解析
8. 如图，△ABC中，∠ACB=90°，D、E是边AB上两点，且CD垂直平分BE，CE平分∠ACD，若BC=2，则AC的长为.

查看试题解析
9. 如图，将等边三角形OAB绕O点按顺时针方向旋转160°，得到三角形OA′B′（点A′，B′分别是点A，B的对应点），则∠1=度；

查看试题解析
10. 如图，等腰△ABC中，AB=AC，∠DBC=15°，AB的垂直平分线MN交AC于点D，则∠A的度数是．

查看试题解析
11. 初三的几位同学拍了一张合影作为留念，已知拍一张底片需要 5 元，洗一张相片需要0.5元．拍一张照片，在每位同学得到一张相片的前提下，平均每人分摊的钱不足1.5元，那么参加合影的同学人数至少为．

查看试题解析
12. 已知如图等腰△ABC ， AB=AC ， ∠BAC=120°，AD⊥BC于点D ，点N是BA延长线上一点，点M是线段AD上一点，MN=MC ，下列结论中正确的结论序号是．
①∠ACM=∠ANM；②∠ANM+∠NCB=90°；③NC=NM；④AM+AN=AB ．

查看试题解析

三、解答题

13. 计算：解下列不等式（组），并把解集在数轴上表示出来．

(1)、 ${\begin{array}{l} x + 6 \leq 3 x + 4 \\ \frac{1 + 2 x}{3} > x - 1 \end{array}$

(2)、 ${\begin{array}{l} 3 (x - 1) < 5 x + 1 \\ \frac{x - 1}{2} \geq 2 x - 4 \end{array}$

查看试题解析
14. 已知不等式5x﹣2＜6x+1的最小正整数解是方程3x﹣ $\frac{3}{2}$ ax=6的解，求a的值．

查看试题解析
15. 如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A(－3，2)，B(0，4)，C(0，2)．

(1)、将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A₁B₁C；平移△ABC ，若A的对应点A₂的坐标为(0，4)，画出平移后对应的△A₂B₂C₂；

(2)、若将△A₁B₁C绕某一点旋转可以得到△A₂B₂C₂ ，请直接写出旋转中心的坐标．

查看试题解析
16. 如图，在△ABC中，AB＝AC ， D为BC上一点，∠B＝30°，连接AD ．

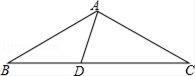(1)、若∠BAD＝45°，求证：△ACD为等腰三角形；

(2)、若△ACD为直角三角形，求∠BAD的度数．

查看试题解析
17. 如图，直线 $y_{1} = - \frac{1}{3} x + b$ 与x轴交于点A ，与y轴交于点B ，与直线 $y_{2} = x$ 交于点E ，点E的横坐标为3．

(1)、求出b的值；

(2)、y轴上有点M ，使得△ABM是等腰三角形，写出所有可能的点M的坐标；

查看试题解析
18. 为加快“秀美荆河水系生态治理工程”进度，污水处理厂决定购买10台污水处理设备．现有A ， B两种型号的设备，每台的价格分别为a万元，b万元，每月处理污水量分别为240吨，200吨．已知购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．

(1)、求a ， b的值；

(2)、厂里预算购买污水处理设备的资金不超过105万元，你认为有哪几种购买方案；

(3)、在（2）的条件下，若每月要求处理污水量不低于2040吨，为了节约资金，请你为污水处理厂设计一种最省钱的购买方案．

查看试题解析
19. 如图1，已知△ABC中，AB=AC，点D是△ABC外一点(与点A分别在直线BC两侧).且DB=DC，过点D作DE//AC，交射线AB于E，连接AD交BC于F.

(1)、求证：AD垂直BC；

(2)、如图1，点E在线段AB上且不与B重合时，求证：DE=AE；

(3)、如图2，当点E在线段AB的延长线上时，请直接写出线段DE，AC，BE的数量关系.

查看试题解析
20. 如图1，已知Rt△ABC中，AB＝BC，AC＝2，把一块含30°角的三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE，长直角边为DF)，点C在DE上，点B在DF上．

(1)、求重叠部分△BCD的面积；

(2)、如图2，将直角三角板DEF绕D点按顺时针方向旋转30度，DE交BC于点M，DF交AB于点N.
①求证：DM＝DN；

②在此条件下重叠部分的面积会发生变化吗？若发生变化，请求出重叠部分的面积，若不发生变化，请说明理由；

(3)、如图3，将直角三角板DEF绕D点按顺时针方向旋转α度(0＜α＜90)，DE交BC于点M，DF交AB于点N，则DM＝DN的结论仍成立吗？重叠部分的面积会变吗？(请直接写出结论，不需要说明理由)

查看试题解析