河北省唐山市路北区2021-2022学年八年级上学期数学期中试卷

试卷更新日期：2021-11-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $a^{2} \cdot a^{3} = a^{5}$ C、 ${(2 a)}^{3} = 6 a^{3}$ D、 $a^{\dot{6}} \div a^{2} = a^{3}$

查看试题解析
2. 如图，若CD是△ABC的中线，AB＝10，则BD＝（　　）

A、6 B、5 C、8 D、4

查看试题解析
3. 下列长度的三条线段能组成三角形的是（）

A、2，1，1 B、3，4，8 C、9，8，5 D、5，6，11

查看试题解析
4. 下面的多边形中，内角和与外角和相等的是（）

A、 B、 C、 D、

查看试题解析
5. 一个缺角的三角形ABC残片如图所示，量得∠A=45°，∠B=60°，则这个三角形残缺前的∠C的度数为（）

A、75° B、65° C、55° D、45°

查看试题解析
6. 如图： $Rt △ A B C ≌ Rt △ D E F$ ，则∠D的度数（）

A、30° B、60° C、45° D、90°

查看试题解析
7. 下列命题中，逆命题是真命题的是（）

A、对顶角相等 B、全等三角形的对应角相等 C、若 $x^{2} = 1$ ，则 $x = 1$ ． D、若 $a = b$ ，则 $a^{2} = b^{2}$

查看试题解析
8. 已知 $8 a^{3} b^{m} \div 28 a^{n} b^{2} = \frac{2}{7} b^{2}$ ，则 $m$ 、 $n$ 的值为（）

A、 $m = 4, n = 3$ B、 $m = 4, n = 1$ C、 $m = 1, n = 3$ D、 $m = 2, n = 3$

查看试题解析
9. 如图，一扇窗户打开后，用窗钩 AB 可将其固定，这里所运用的几何原理是（）

A、两点之间线段最短 B、三角形两边之和大于第三边 C、两点确定一条直线 D、三角形的稳定性

查看试题解析
10. 如图，根据图上标注的信息，则 $α$ 的大小（）

A、100° B、105° C、115° D、120°

查看试题解析
11. 下列各图中a、b、c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（）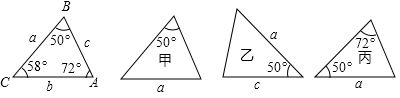

A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙

查看试题解析
12. 一个多边形的内角和比它的外角和的3倍少180°，这个多边形共有（）对角线．

A、9条 B、14条 C、20条 D、27条

查看试题解析
13. 如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于D ．若BC＝32，且CD∶BD＝7∶9，则点D到边AB的距离为（）

A、7 B、9 C、14 D、18

查看试题解析
14. 如图，在长方形ABCD中， $A D = 2 A B = 6$ ，E为BC边上一点，且 $C E = 2$ ，连接DE ，动点P从点B出发，以每秒1个单位的速度沿着 $B C - C D - D A$ 运动，到达点A立即停止，运动时间记为t秒，当 $△ A B P$ 与 $△ D C E$ 全等时，t的值为（）

A、2 B、3 C、3或13 D、2或13

查看试题解析

二、填空题

15. 计算： ${(- a)}^{4} \cdot {(- a)}^{3} =$ ．

查看试题解析
16. 在直角 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点D，若 $C D = 6$ ，则点D到斜边 $A B$ 的距离为．

查看试题解析
17. 若n为正整数，且 $x^{2 n} = 3$ ，则 ${(x^{3 n})}^{2}$ 的值为．

查看试题解析
18. 如图，AB=12m，CA⊥AB于点A，DB⊥AB于点B，且AC=4m，点P从点B以1m/min的速度向点A运动；点Q从点B以2m/min的速度向点D运动，P，Q两点同时出发，运动min时，△CAP与△PBQ全等．

查看试题解析

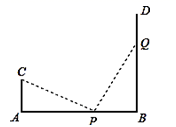
三、解答题

19. 计算：

(1)、 ${(a b^{2})}^{2} \cdot {(- a^{3} b)}^{3} \div (- 5 a b)$ ；

(2)、 ${(a + 3)}^{2} + (a + 1) (a - 1) - 2 (2 a + 4)$ ；

查看试题解析
20. 先化简，再求值： $[{(x - 2 y)}^{2} - (x - y) (x + y) - x^{2} y + 4 x y] \div 2 y$ ，其中 $x = - 2$ ， $y = 2$ ．

查看试题解析
21. 已知一个n边形的每一个外角都等于30°．

(1)、求n的值．

(2)、求这个n边形的内角和．

查看试题解析
22. 某学校有一块长方形活动场地，长为2x米，宽比长少5米．实施“阳光体育”行动以后，学校为了扩大学生的活动场地，让学生能更好地进行体育活动，将操场的长和宽都增加了4米．

(1)、求扩大后学生的活动场地的面积．（用含x的代数式表示）

(2)、若x＝20，求活动场地扩大后增加的面积．

查看试题解析
23. 尺规作图，保留作图痕迹，不写作法．

⑴作△ABC中∠B的平分线；

⑵作△ABC边BC上的高．

查看试题解析
24. 如图，在 $△ A B C$ 中， $A E$ 为边 $B C$ 上的高，点D为边 $B C$ 上的一点，连接 $A D$ ．

(1)、当 $A D$ 为边 $B C$ 上的中线时，若 $A E = 6$ ， $△ A B C$ 的面积为30，求 $C D$ 的长；

(2)、当 $A D$ 为 $∠ B A C$ 的角平分线时，若 $∠ C = 66 °$ ， $∠ B = 36 °$ ，求 $∠ D A E$ 的度数．

查看试题解析
25. 如图，点E在CD上，BC与AE交于点F，AB=CB，BE=BD，∠1=∠2.

(1)、求证： $△ A B E ≅ △ C B D$ ；

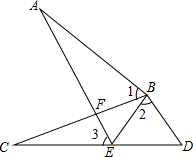(2)、求证：∠1=∠3.

查看试题解析
26. 如图，在四边形ABCD中，AD＝BC＝4，AB＝CD，BD＝6，点E从D点出发，以每秒1个单位的速度沿DA向点A匀速移动，点F从点C出发，以每秒3个单位的速度沿C→B→C作匀速移动，点G从点B出发沿BD向点D匀速移动，三个点同时出发，当有一个点到达终点时，其余两点也随之停止运动．

(1)、试证明：AD∥BC．

(2)、在移动过程中，小芹发现当点G的运动速度取某个值时，有△DEG与△BFG全等的情况出现，请你探究当点G的运动速度取哪些值时，△DEG与△BFG全等．

查看试题解析