江苏省无锡市锡山区锡东片2021-2022学年七年级上学期数学期中考试试卷

试卷更新日期：2021-11-19 类型：期中考试

进入出卷网下载

一、单选题

1. -3的相反数是（）

A、3 B、-3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 夏新同学上午卖废品收入13元，记为+13元，下午买旧书支出9元，记为（）元.

A、+4 B、﹣9 C、﹣4 D、+9

查看试题解析
3. 青藏高原是世界上海拔最高的高原，它的面积是 2500000 平方千米．将 2500000 用科学记数法表示应为（）

A、 $0.25 \times 10^{7}$ B、 $2.5 \times 10^{7}$ C、 $2.5 \times 10^{6}$ D、 $25 \times 10^{5}$

查看试题解析
4. 在下列各数 $1. \overset{•}{3}$ ， $π$ ，0， $\frac{22}{7}$ ，1.010010001，－3.14， $0.262662666 \cdot \cdot \cdot$ （每两个2之间依次增加一个数6）中，无理数的个数有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
5. 下列各组中的两个项不属于同类项的是（）

A、3x²y和－2x²y B、a²和3² C、－1和1 $\frac{1}{4}$ D、－xy和2yx

查看试题解析
6. 下列计算正确的是（）

A、 $7 a + a = 7 a^{2}$ B、 $3 x^{2} y - 2 x^{2} y = x^{2} y$ C、 $5 y - 3 y = 2$ D、 $3 a + 2 b = 5 a b$

查看试题解析
7. 用代数式表示“ $m$ 的7倍与 $n$ 的差的平方”，正确的是（）

A、 $7 m - n^{2}$ B、 ${(7 m - n)}^{2}$ C、 $7 {(m - n)}^{2}$ D、 ${(m - 7 n)}^{2}$

查看试题解析
8. 下列说法：①若 $a$ 为任意有理数，则｜a +1｜的值总是正的；②若ab＞0，a+b＜0，则a＜0，b＜0；③单项式 $- \frac{2}{3} {πx}^{2} y$ 的系数是 $- \frac{2}{3}$ ，次数是4；④ $4 x y - 6 x^{2} y - x y^{3} + 3^{5}$ 是五次四项式.其中错误的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图所示，将形状大小完全相同的“▱”按照一定规律摆成下列图形，第1幅图中“▱”的个数为a₁ ，第2幅图中“▱”的个数为a₂ ，第3幅图中“▱”的个数为a₃ ， …，以此类推， $\frac{2}{a_{1}} + \frac{2}{a_{2}} + \frac{2}{a_{3}} + \frac{2}{a_{4}} + \dots \dots + \frac{2}{a_{2021}}$ 的值为（）

A、 $\frac{2021}{1011}$ B、 $\frac{1011}{2021}$ C、 $\frac{2020}{2021}$ D、 $\frac{2021}{2020}$

查看试题解析
10. “书法艺术课”开课后，某同学买了一包纸练习软笔书法，且每逢星期几写几张，即每星期一写1张，每星期二写2张，……，每星期日写7张，若该同学从某年的5月1日开始练习，到5月30日练习完后累积写完的宣纸总数超过120张，请推断出5月30日可能是星期几（）

A、二、三、四 B、三、四、五 C、四、五、六 D、五、六、日

查看试题解析

二、填空题

11. ﹣ $\frac{2}{3}$ 的倒数是．

查看试题解析
12. 比较大小： $- \frac{2}{3}$ $- \frac{3}{4}$ ； $- (- 3)$ $- | - 3 |$ (填“＞”，“＜”，“=” )

查看试题解析
13. 在数轴上，与表示-1的点的距离是2的点表示的数是.

查看试题解析
14. 如图所示是计算机程序计算，若开始输入x＝－1，则最后输出的结果是.

查看试题解析
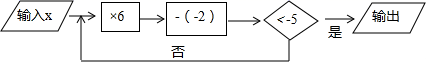15. 已知 $a$ 和 $b$ 互为相反数，c和d互为倒数，m是绝对值最小的数，x是最大的负整数，则 $x^{2021} - 3 c d + \frac{a + b + m}{2021}$ 的值为

查看试题解析
16. 若有理数 $x ， y$ 满足 $| y | = 10$ ， $x^{2} = 64$ ，且 $| x - y | = x - y$ ，则 $x + y$ 的值为.

查看试题解析

17. 某市地铁票价计费标准如表所示：乘车距离x(单位：公里)：

乘车距离x	x≤6	6＜x≤12	12＜x≤22	22＜x≤32	x＞32
票价（元）	3	4	5	6	每增加1元可乘20公里

另外，使用市政交通一卡通，每个自然月每张卡片支出累计满100元后，超出部分打8折；满150元后，超出部分打5折；支出累计达400元后，不再打折.小红妈妈上班时，需要乘坐地铁15公里到达公司，每天上下班共乘坐两次，如果每次乘坐地铁都使用市政交通一卡通，那么每月第22次乘坐地铁上下班时，她刷卡支出的费用是元.

查看试题解析

18. 当x=时，4-｜x｜-｜x-1｜-｜x+2｜-｜x-3｜-｜x+1｜的值是.

查看试题解析

三、解答题

19. 在数轴上表示下列各数，并用“＜”把它们按从小到大的顺序排列.
$- 2^{2}$ ， $- (- 1)$ ，0， $- | - 2 |$ ， $3 \frac{1}{2}$

查看试题解析
20. 计算：

(1)、 $- 4 + (- 5) - (- 1)$

(2)、 $3 - 2^{3} \div 4 \times (- \frac{1}{4})$

(3)、 $- 24 \times (- \frac{1}{2} + \frac{3}{4} - \frac{2}{3})$

(4)、 $- 2^{3} + | 2 - 3 | - 2 \times {(- 1)}^{2013}$

查看试题解析
21. 化简：

(1)、 $2 a^{2} - 3 a b - 14 a^{2} + 4 a b$

(2)、 $- 2 (2 x^{2} - x y) + 4 (x^{2} + x y - 1)$

查看试题解析
22. 化简求值： $7 a^{2} b + 2 (2 a^{2} b - 3 a b^{2})$ $- 3 (4 a^{2} b - a b^{2})$ ，其中 $a ， b$ 满足 $| a + 2 | + {(b - \frac{1}{2})}^{2} = 0$ .

查看试题解析
23. 已知有理数a、b、c在数轴上的位置：

(1)、a＋b0；a＋c0；b－c0（用“＞，＜，=”填空）

(2)、试化简|a＋b|－2|a＋c|－|b－c|.

查看试题解析
24. 定义一种新运算，观察以下式子：1⊙3=1×4﹣3=1；3⊙（﹣1）=3×4+1=13；5⊙4=5×4﹣4=16；4⊙（﹣3）=4×4+3=19.

(1)、请用含a、b的代数式表示：a⊙b=；

(2)、若a≠b，那么 a⊙bb⊙ a（填入“=”或“≠”）

(3)、若a⊙（2b）﹣1=3，请计算2+[（b﹣a）⊙（2a+b）]的值.

查看试题解析
25. （感悟数学方法）
已知： $A = 2 a b - a$ ， $B = - a b + 2 a + b$ .

(1)、计算： $5 A - 2 B$ ；

(2)、若 $5 A - 2 B$ 的值与字母b的取值无关，求a的值.

(3)、（解决实际问题）请利用上述问题中的数学方法解决下面问题：

新冠疫情期间，某医药器材经销商计划同时购进一批甲、乙两种型号的口罩.已知甲型号口罩每箱进价为800元，乙型号口罩每箱进价为600元.该医药公司根据疫情，决定购进两种口罩共20箱，有多种购进方案，现销售一箱甲型口罩，利润率为45%，乙型口罩的售价为每箱1000元.而且为了及时控制疫情，公司决定每售出一箱乙型口罩，返还顾客现金m元，甲型口罩售价不变，要使不同方案所购进的口罩全部售出后经销商最终获利相同，求m的值.

查看试题解析
26. 如图，甲、乙两人（看成点）分别在数轴﹣3和5的位置上，沿数轴做移动游戏.每次移动游戏规则：裁判先捂住一枚硬币，再让两人猜向上一面是正是反，而后根据所猜结果进行移动.
①若都对或都错，则甲向东移动1个单位，同时乙向西移动1个单位；

②若甲对乙错，则甲向东移动4个单位，同时乙向东移动2个单位；

③若甲错乙对，则甲向西移动2个单位，同时乙向西移动4个单位.

(1)、若两人完成了2次移动游戏第一次甲、乙都错，第二次甲对乙错，此时甲、乙两人的距离为；

(2)、从如图的位置开始，若完成了10次移动游戏，发现甲、乙每次所猜结果均为一对一错.设乙猜对n次，则他最终停留的位置对应的数是什么？试用含n的代数式表示，并求该位置距离原点O最近时n的值；

(3)、从如图的位置开始，若进行了k次移动游戏后，甲与乙的位置相距2个单位，直接写出k的值.

查看试题解析