广西南宁普通高中2022届高三上学期文数11月教学质量检测试卷

试卷更新日期：2021-11-18 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知集合 $A = {(x ， y) | y = - x + 2}$ ， $B = {(x ， y) | y = 2^{x}}$ ，则 $A \cap B$ 元素的个数为

A、0 B、1 C、2 D、3

查看试题解析
2. 已知向量 $\vec{a} ， \vec{b} ， \vec{c}$ 共面，且均为单位向量， $\vec{a} \cdot \vec{b} = 0$ ，则 $| \vec{a} + \vec{b} + \vec{c} |$ 的取值范围是（）

A、 $[\sqrt{2} - 1 ， \sqrt{2} + 1]$ B、 $[1 ， \sqrt{2}]$ C、 $[\sqrt{2} ， \sqrt{3}]$ D、 $[\sqrt{2} - 1 ， 1]$

查看试题解析
3. “ $θ$ 为第一或第四象限角”是“ $\cos θ > 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 已知a，b，c∈R，若 $\frac{b}{a}$ · $\frac{c}{a}$ >1，且 $\frac{b}{a} + \frac{c}{a} \geq - 2$ ，则下列结论成立的是（）

A、a，b，c同号 B、b，c同号，a与b，c异号 C、b，c同号，a不能确定 D、a，b，c是否同号都不能确定

查看试题解析
5. 哥尼斯堡“七桥问题”是著名的古典数学问题，它描述的是：在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来(如图1).问是否可能从这四块陆地中任一块出发，恰好通过每座桥一次，再回到起点?瑞士数学家欧拉于1736年研究并解决了此问题，他把该问题归结为如图2所示的“一笔画”问题，并证明了上述走法是不可能的.假设在图2所示七条线中随机选取两条不同的线，则这两条线都与A直接相连的概率为（）

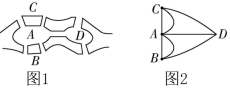A、 $\frac{2}{7}$ B、 $\frac{3}{7}$ C、 $\frac{1}{2}$ D、 $\frac{10}{21}$

查看试题解析
6. 在 $Δ A B C$ 中，角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ， $S$ 表示 $Δ A B C$ 的面积，若 $S = \frac{1}{4} (b^{2} + c^{2} - a^{2})$ ，则 $∠ A =$ （）

A、 $90 °$ B、 $60 °$ C、 $45 °$ D、 $30 °$

查看试题解析
7. 若1路、2路公交车的站点均包括泉港一中，且1路公交车每10分钟一趟，2路公交车每20分钟一趟，则某学生去坐这2趟公交车回家，等车不超过5分钟的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{3}{5}$ C、 $\frac{5}{8}$ D、 $\frac{7}{8}$

查看试题解析
8. 已知 $P$ 为双曲线 $\frac{y^{2}}{4} - x^{2} = 1$ 上任一点，过 $P$ 点向双曲线的两条渐进线分别作垂线，垂足分别为 $A$ ， $B$ ，则 $| P A | \cdot | P B |$ 的值为（）

A、4 B、5 C、 $\frac{4}{5}$ D、与点 $P$ 的位置有关

查看试题解析
9. 已知函数f(x)=3 $\sqrt{3} sin \frac{x}{4}$ cos $\frac{x}{4}$ +3cos² $\frac{x}{4}$ +m在[0，2π]上的最小值为 $- \frac{3}{2}$ ，点A为函数f(x)的图象在y轴右侧的第一个最高点，点B为函数f(x)的图象在y轴右侧的第二个对称中心，O为坐标原点，则tan∠BAO=（）

A、- $\frac{11 π}{2 π^{2} - 9}$ B、- $\frac{11}{2 π - 9}$ C、 $\frac{9}{2 π}$ D、 $\frac{1}{π}$

查看试题解析
10. 如图，在四面体VABC中，已知VA⊥平面VBC，VA与平面ABC所成的角为45°，D是BC上一动点，设直线VD与平面ABC所成的角为θ，则（）

A、θ≤60° B、θ≥30° C、θ≤45° D、θ≤75°

查看试题解析
11. 已知数列{an}满足：a1＝1， $a_{n + 1} = \frac{a_{n}}{a_{n} + 2}$ (n∈N*)．若 ${}^{b}n ＋ 1 ＝ (n － 2 λ) (\frac{1}{a_{n}} + 1)$ (n∈N*)，b1＝－ $\frac{3}{2}$ λ，且数列{bn}是单调递增数列，则实数λ的取值范围是（）

A、λ< $\frac{4}{5}$ B、λ<1 C、λ< $\frac{3}{2}$ D、λ< $\frac{2}{3}$

查看试题解析
12. 已知函数f(x)= $\sqrt{3}$ (sin2x+4cosx)+2sinx，则f(x)的最大值为（）

A、4 $\sqrt{3}$ B、 $\frac{17}{2}$ C、6 D、5 $\sqrt{3}$ +2

查看试题解析

二、填空题

13. 12本相同的资料书配给三个班级，要求每班至少一本且至多六本，则不同的分配方法共有种．

查看试题解析
14. ${(\frac{2}{x} - x - 1)}^{3}$ 的展开式中， $x$ 的系数为（用数字作答）.

查看试题解析
15. 抛物线 $y^{2} = 8 x$ 的焦点为 $F$ ，点 $A (6 ， 3) ， P$ 为抛物线上一点，且 $P$ 不在直线 $A F$ 上，则 $Δ P A F$ 周长的最小值为．

查看试题解析
16. 宋元时期著名数学家朱世杰在其巨著《四元玉鉴》中利用“招差术”得到以下公式： $\overset{n}{\sum_{k = 1}}$ k(k+1)= $\frac{1}{3}$ n(n+1)(n+2).具体原理如下：∵k(k+1)= $\frac{1}{3}$ k(k+1)[(k+2)-(k-1)]= $\frac{1}{3}$ [k·(k+1)(k+2)-(k-1)k(k+1)]，
∴ $\overset{n}{\sum_{k = 1}}$ k(k+1)= $\frac{1}{3}$ {1×2×3+(2×3×4-1×2×3)+…+[n(n+1)(n+2)-(n-1)n(n+1)]}= $\frac{1}{3}$ n(n+1)(n+2).

类比上述方法， $\overset{n}{\sum_{k = 1}}$ k(k+1)(k+2)=.

查看试题解析

三、解答题

17. 在 $△ A B C$ 中，内角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ，若 $sin (A + C) = 2 sin A cos (A + B)$ ，且 ${sin}^{2} A + {sin}^{2} B - {sin}^{2} C + \sqrt{2} sin A sin B = 0$ .

(1)、求证： $a ， b ， 2 a$ 成等比数列；

(2)、若 $△ A B C$ 的面积是2，求 $c$ 边的长.

查看试题解析
18. 如图，直三棱柱ABC-A₁B₁C₁中，D，E分别是AB，BB₁的中点，AA₁=AC=CB= $\frac{\sqrt{2}}{2}$ AB．

(1)、证明：BC₁∥平面A₁CD；

(2)、求异面直线BC₁和A₁D所成角的大小；

(3)、当AB=2 $\sqrt{2}$ 时，求三棱锥C-A₁DE的体积.

查看试题解析

19. 成都市现在已是拥有1400多万人口的城市，机动车保有量已达450多万辆，成年人中约

40 %

拥有机动车驾驶证．为了解本市成年人的交通安全意识情况，某中学的同学利用国庆假期进行了一次全市成年人安全知识抽样调查．先根据是否拥有驾驶证，用分层抽样的方法抽取了200名成年人，然后对这200人进行问卷调查．这200人所得的分数都分布在

[30 ， 100]

范围内，规定分数在80以上（含80）的为“具有很强安全意识”，所得分数的频率分布直方图如图所示．

	拥有驾驶证	没有驾驶证	总计
具有很强安全意识
不具有很强安全意识	58
总计			200

(1)、补全上面的

2 \times 2

列联表，并判断能否有超过

95 %

的把握认为“具有很强安全意识”与拥有驾驶证有关？

(2)、将上述调查所得的频率视为概率，现从全市成年人中随机抽取4人，记“具有很强安全意识”的人数为X，求X的分布列及数学期望．

附表及公式： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ ．

P（ $K^{2} \geq k_{0}$ ）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
$k_{0}$	2.072	2.706	3.841	5.024	6.635	7.879	10.828

查看试题解析

20. 已知函数 $f (x) = {(x - a)}^{2} \ln x ， a \in R$ ．

(1)、若 $a = 3 \sqrt{e}$ ，其中 $e$ 为自然对数的底数，求函数 $g (x) = \frac{f (x)}{x}$ 的单调区间；

(2)、若函数 $f (x)$ 既有极大值，又有极小值，求实数 $a$ 的取值范围．

查看试题解析
21. 设F₁ ， F₂分别是椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1(a>b>0)的左，右焦点，M是C上一点且MF₂与x轴垂直，直线MF₁与C的另一个交点为N.

(1)、若直线MN的斜率为 $\frac{3}{4}$ ，求C的离心率；

(2)、若直线MN在y轴上的截距为2，且|MN|=5|F₁N|，求a，b.

查看试题解析
22. 已知直线 $l$ 的极坐标方程是 $ρ \sin (θ - \frac{π}{3}) = 0$ ,以极点为平面直角坐标系的原点,极轴为 $x$ 轴的正半轴，建立平面直角坐标系,曲线C的参数方程是 ${\begin{array}{l} x = 2 \cos α \\ y = 2 + 2 \sin α \end{array}$ ,（ $α$ 为参数）.

(1)、求直线 $l$ 被曲线C截得的弦长；

(2)、从极点作曲线C的弦,求各弦中点轨迹的极坐标方程.

查看试题解析