广东省惠州市2022届高三上学期数学第二次调研(10月)试卷
试卷更新日期:2021-11-18 类型:月考试卷
一、单选题
-
1. 已知 是虚数单位,复数 的虚部为( )A、-1 B、0 C、1 D、2. 已知全集 ,集合 , ,则 ( )A、 B、 C、 D、3. “x<0”是“ln(x+1)<0”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 已知 , 为两条不同的直线, , 为两个不同的平面,则下列说法正确的是( )A、若 , ,则 B、若 , ,则 C、若 , , ,则 D、若 , ,则5. 已知 ,则函数 的最小值为( )A、-1 B、0 C、1 D、26. 函数 的图象大致为( )A、
 B、
B、 C、
C、 D、
D、 7. 已知直线 : 与圆 : 的交点为 , ,点 是圆 上一动点,设点 ,则 的最大值为( )A、9 B、10 C、11 D、128. 某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度d(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度l对保温效果的影响,利用热传导定律得到热传导量q满足关系式 ,其中玻璃的热传导系数 焦耳/(厘米·度),不流通、干燥空气的热传导系数 焦耳/(厘米·度), 为室内外温度差,q值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
7. 已知直线 : 与圆 : 的交点为 , ,点 是圆 上一动点,设点 ,则 的最大值为( )A、9 B、10 C、11 D、128. 某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度d(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度l对保温效果的影响,利用热传导定律得到热传导量q满足关系式 ,其中玻璃的热传导系数 焦耳/(厘米·度),不流通、干燥空气的热传导系数 焦耳/(厘米·度), 为室内外温度差,q值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:型号
每层玻璃厚度d(单位:厘米)
玻璃间夹空气层厚度l(单位:厘米)
A型
0.4
3
B型
0.3
4
C型
0.5
3
D型
0.4
4
则保温效果最好的双层玻璃的型号是( )
A、A型 B、B型 C、C型 D、D型二、多选题
-
9. 记等差数列 的前 项和为 ,已知 , ,则有( )A、 B、 C、 D、10. 某种产品的价格 (单位:元/ )与需求量 (单位:kg)之间的对应数据如下表所示:
10
15
20
25
30
11
10
8
6
5
根据表中的数据可得回归直线方程为 ,则以下结论正确的是( )
A、 与 正相关 B、 与 负相关 C、样本中心为 D、该产品价格为35元/kg时,日需求量大约为11. 已知函数 ,若 ,且 的最小值为 ,则下列说法正确的是( )A、 B、函数 在 上单调递增 C、将函数 的图象向右平移 个单位长度后得到的图象关于 轴对称 D、对 ,都有12. 如图所示,从一个半径为 (单位:m)的圆形纸板中切割出一块中间是正方形,四周是四个正三角形的纸板,以此为表面(舍弃阴影部分)折叠成一个正四棱锥 ,则以下说法正确的是( )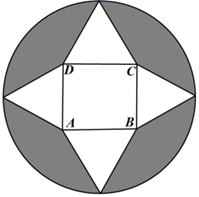 A、四棱锥 的体积是 B、四棱锥 的外接球的表面积是 C、异面直线 与 所成角的大小为 D、二面角 所成角的余弦值为
A、四棱锥 的体积是 B、四棱锥 的外接球的表面积是 C、异面直线 与 所成角的大小为 D、二面角 所成角的余弦值为三、填空题
-
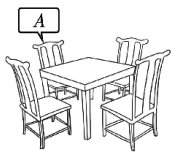
13. 已知 ,则 .14. 一张方桌有四个座位, 先坐在如图所示的座位上, , , 三人随机坐到其他三个位置上,则 与 相邻的概率为.
 15. 根据抛物线的光学性质可知,从抛物线的焦点发出的光线经该抛物线反射后与对称轴平行.如图所示,沿直线 发出的光线经抛物线 反射后,与 轴相交于点 ,则 .
15. 根据抛物线的光学性质可知,从抛物线的焦点发出的光线经该抛物线反射后与对称轴平行.如图所示,沿直线 发出的光线经抛物线 反射后,与 轴相交于点 ,则 . 16. 已知 ,若 ,则函数 的单调递增区间是;若不等式 对 恒成立,则实数 的取值范围为.
16. 已知 ,若 ,则函数 的单调递增区间是;若不等式 对 恒成立,则实数 的取值范围为.四、解答题
-
17. 已知数列 是公比为2的等比数列,其前 项和为 , , , 成等差数列.(1)、求数列 的通项公式;(2)、令 ,求数列 的前 项和 .18. 在 中,内角 , , 的对边分别为 , , ,已知 .(1)、求 ;(2)、若 是锐角三角形,且 ,求边长 的取值范围.19. 如图所示的多面体是由一个直四棱柱被平面 所截后得到的,其中 , , .
 (1)、求证: 平面 ;(2)、求直线 与平面 所成角的正弦值.20. 一家养鸡场养了甲、乙两个品种的产蛋鸡,在甲、乙两个品种的产蛋鸡中各随机抽取1000只,分别记录其日产蛋量.根据产蛋期的记录,绘制了日产蛋量的频率分布直方图,如图所示(视频率为概率).
(1)、求证: 平面 ;(2)、求直线 与平面 所成角的正弦值.20. 一家养鸡场养了甲、乙两个品种的产蛋鸡,在甲、乙两个品种的产蛋鸡中各随机抽取1000只,分别记录其日产蛋量.根据产蛋期的记录,绘制了日产蛋量的频率分布直方图,如图所示(视频率为概率).
 (1)、若甲、乙两种鸡的日产蛋量相互独立,记“甲、乙两种鸡的日产蛋量都不低于850个”为事件 ,试估计事件 发生的概率;(2)、由于甲、乙两种鸡的食量和产蛋的大小不同,甲品种1000只鸡的日产蛋量小于850个的利润率为 ,日产蛋量不小于850个而小于900个的利润为 ,日产蛋量不小于900个的利润率为 ;乙品种1000只鸡的日产蛋量小于850个的利润率为 ,日产蛋量不小于850个而小于900个的利润为 ,日产蛋量不小于900个的利润率为 .若在甲、乙两个品种上各投资10万元, (单位:万元)和 (单位:万元)分别表示投资甲、乙两个品种所获得的利润,求 和 的数学期望,并对甲、乙两个品种的投资进行分析比较.
(1)、若甲、乙两种鸡的日产蛋量相互独立,记“甲、乙两种鸡的日产蛋量都不低于850个”为事件 ,试估计事件 发生的概率;(2)、由于甲、乙两种鸡的食量和产蛋的大小不同,甲品种1000只鸡的日产蛋量小于850个的利润率为 ,日产蛋量不小于850个而小于900个的利润为 ,日产蛋量不小于900个的利润率为 ;乙品种1000只鸡的日产蛋量小于850个的利润率为 ,日产蛋量不小于850个而小于900个的利润为 ,日产蛋量不小于900个的利润率为 .若在甲、乙两个品种上各投资10万元, (单位:万元)和 (单位:万元)分别表示投资甲、乙两个品种所获得的利润,求 和 的数学期望,并对甲、乙两个品种的投资进行分析比较.