福建省宁德市重点高中2022届高三上学期数学10月月考试卷

试卷更新日期：2021-11-18 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知 $a \in R$ ，则“ $a > 1$ ”是“ $\frac{1}{a} < 1$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
2. 已知 $a = x^{2} + \frac{1}{4 x^{2}}$ ， $b = π^{- 0.1}$ ， $c = \log_{3} [(2 - t) t]$ ，则 $a$ ， $b$ ， $c$ 的大小关系为（）

A、 $a > b > c$ B、 $b > a > c$ C、 $c > b > a$ D、 $a > c > b$

查看试题解析
3. 2018年元旦期间，某高速公路收费站的三个高速收费口每天通过的小汽车数 $X$ （单位：辆）均服从正态分布 $N (600 ， σ^{2})$ ．若 $P (500 < X \leq 700) = 0.6$ ，假设三个收费口均能正常工作，则这三个收费口每天通过的小汽车数至少有一个超过700辆的概率为（）

A、 $\frac{1}{125}$ B、 $\frac{12}{125}$ C、 $\frac{61}{125}$ D、 $\frac{64}{125}$

查看试题解析
4. 若 ${(2 x + 1)}^{8} = a_{0} + a_{1} (x + 1) + a_{2} {(x + 1)}^{2} + \dots + a_{8} {(x + 1)}^{8}$ ，则 $a_{3} =$ （）

A、56 B、448 C、-56 D、-448

查看试题解析
5. 如图，直线 $x = m (m > 1)$ 依次与曲线 $y = \log_{a} x$ 、 $y = \log_{b} x$ 及x轴相交于点A、点B及点C，若B是线段 $A C$ 的中点，则（　　）

A、 $1 < b \leq 2 a - 1$ B、 $b > 2 a - 1$ C、 $1 < b \leq 2 a$ D、 $b > 2 a$

查看试题解析
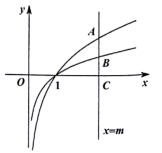6. 2021年1月初，河北某区域的“新冠疫情”出现明显反弹，相关部门紧急从 $Ｈ$ 省抽调包括甲、乙在内的七名医疗专家进驻该区域的三个疫情“高风险”地区进行协助防控，要求每个地区至少安排两名专家，则甲、乙两名专家安排在不同地区的概率为（）

A、 $\frac{16}{21}$ B、 $\frac{10}{21}$ C、 $\frac{13}{14}$ D、 $\frac{9}{14}$

查看试题解析
7. 已知函数 $f (x) = a - x^{2} (\frac{1}{e} \leq x \leq e)$ 与 $g (x) = 2 \ln x$ 的图象上存在关于 $x$ 轴对称的点，则 $a$ 的取值范围是（）

A、 $[1 ， \frac{1}{e^{2}} + 2]$ B、 $[\frac{1}{e^{2}} + 2 ， e^{2}]$ C、 $[1 ， e^{2} - 2]$ D、 $[e^{2} - 2 ， + \infty]$

查看试题解析
8. 已知定义在 $R$ 上的函数 $f (x)$ 满足， $2 f (x) + f^{'} (x) > 0$ 且有 $f (\frac{1}{2}) = \frac{1}{e}$ ，则 $f (x) > \frac{1}{e^{2 x}}$ 的解集为（）

A、 $(0 ， \frac{1}{2})$ B、 $(\frac{1}{2} ， + \infty)$ C、 $(0 ， 2)$ D、 $(0 ， + \infty)$

查看试题解析

二、多选题

9. 某数学课外兴趣小组对函数 $f (x) = \lg \frac{x^{2} + 1}{| x |} (x \neq 0 ， x \in R)$ 的性质进行了探究，得到下列四个命题，其中真命题为（）

A、函数 $f (x)$ 的图象关于 $y$ 轴对称 B、当 $x > 0$ 时， $f (x)$ 是增函数，当 $x < 0$ 时， $f (x)$ 是减函数 C、函数 $f (x)$ 的最小值是 $\lg 2$ D、当 $- 1 < x < 0$ 或 $x > 1$ 时， $f (x)$ 是增函数

查看试题解析
10. 已知定义域为 $R$ 的函数 $f (x)$ 满足 $f (x - 1)$ 是奇函数， $f (x + 1)$ 为偶函数，当 $- 1 < x \leq 1$ 时， $f (x) = x^{2}$ ，则（）

A、函数 $f (x)$ 不是偶函数 B、函数 $f (x)$ 的最小正周期为4 C、函数 $f (x)$ 在 $[- 2 ， 2]$ 上有3个零点 D、 $f (5) > f (4)$

查看试题解析
11. 已知 $a > 0 ， b > 0 ， a + b^{2} = 1$ ，则下列选项中正确的是（）

A、 $3^{a - b}$ 的最大值为 $3$ B、 $b \sqrt{a}$ 的最大值为 $\frac{1}{2}$ C、 $\sqrt{a} + b$ 的最大值为 $\sqrt{2}$ D、 $\frac{1}{a + 1} + \frac{1}{b^{2}}$ 的最小值为 $2$

查看试题解析
12. 若存在正数 $t$ 满足 $a (2 e - t) \ln t = 1$ ，则实数 $a$ 可能的取值为（）

A、-2 B、 $\frac{1}{e^{2}}$ C、 $\frac{1}{e}$ D、2

查看试题解析

三、填空题

13. 已知 $f (x)$ 是定义在R上且周期为4的奇函数，当 $x \in (2 ， 4]$ 时， $f (x) = - x^{2} + 7 x - 12$ ，则 $f (2021)$ 的值是．

查看试题解析
14. 小红同学去买糖果，现只有四种不同口味的糖果可供选择，单价均为一元一颗，小红只有7元钱，要求钱全部花完且每种糖果都要买，则不同的选购方法共有种．（用数字作答）

查看试题解析
15. 已知函数 $f (x) = {\begin{array}{l} e^{x} ， x \in [- 1 ， 1) \\ - | x^{2} - 1 | + 2 ， x \in [1 ， 3] \end{array}$ ，函数 $g (x) = k x + 2$ ，若 $f (x) = g (x)$ ， $x \in [- 1 ， 3]$ 恰有两个零点，则 $k^{2} + 2 k$ 的取值范围是．

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} - x^{2} - 4 x + 1 ， x \leq 0 \\ | \log_{\frac{1}{3}} x | ， x > 0 \end{array}$ ，若方程 $f (x) = a$ 有四个不同的解 $x_{1} ， x_{2} ， x_{3} ， x_{4}$ ，且 $x_{1} < x_{2} < x_{3} < x_{4}$ ，则实数 $a$ 的取值范围是， $x_{4} \cdot (x_{1} + x_{2}) + \frac{3}{x_{3} \cdot x_{4}^{2}}$ 的最大值是.

查看试题解析

四、解答题

17. 已知函数 $f (x) = x^{3} + a x^{2} + b x + c$ 在 $x = - \frac{2}{3}$ 与 $x = 1$ 处都取得极值．

(1)、求 $a$ ， $b$ 的值；

(2)、若对任意 $x \in [- 1 ， 2]$ ，不等式 $f (x) < c^{2}$ 恒成立，求实数 $c$ 的取值范围．

查看试题解析
18. 已知函数 $f (x) = \ln (x + t)$ .

(1)、当 $t = 1$ 时，求不等式 $f (2 x) - f (x + 1) < 0$ 的解集

(2)、当 $t = e$ 时，若关于 $x$ 的不等式 $f (x) > 2^{- x} + m$ 在 $[0 ， 2]$ 上有解，求 $m$ 的取值范围.

查看试题解析
19. 甲、乙两队进行排球比赛，每场比赛采用“5局3胜制”（即有一支球队先胜3局即获胜，比赛结束）．比赛排名采用积分制，积分规则如下：比赛中，以 $3 ： 0$ 或 $3 ： 1$ 取胜的球队积3分，负队积0分；以 $3 ： 2$ 取胜的球队积2分，负队积1分，已知甲、乙两队比赛，甲每局获胜的概率为 $\frac{2}{3}$ ．

(1)、甲、乙两队比赛1场后，求甲队的积分 $X$ 的概率分布列和数学期望；

(2)、甲、乙两队比赛2场后，求两队积分相等的概率．

查看试题解析
20. 已知函数 $f (x) = x^{2} + b x + c$ ，（ $b$ ， $c \in R$ ）的图象过点 $(1 ， 1)$ ，且对 $\forall x \in R$ ， $f (1 - x) = f (1 + x)$ 恒成立.

(1)、求函数 $f (x)$ 的解析式；

(2)、若对任意的 $x \in [2 ， 16]$ ，不等式 $f (\log_{4} x) \leq m \log_{4} x$ 恒成立，求 $m$ 的最小值.

查看试题解析

21. 某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费

x

(单位：千元)对年销售量

y

(单位：吨)的影响，对近

8

年的年宣传费

x_{i}

和年销售量

y_{i}

(i = 1 ， 2 ， 3 ， \dots ， 8)

数据作了初步处理，得到下面的散点图及一些统计量的值.

$\bar{x}$	$\bar{y}$	$\bar{w}$	$\sum_{i = 1}^{8} {(x_{i} - \bar{x})}^{2}$	$\sum_{i = 1}^{8} {(w_{i} - \bar{w})}^{2}$	$\sum_{i = 1}^{8} (x_{i} - \bar{x}) (y_{i} - \bar{y})$	$\sum_{i = 1}^{8} (w_{i} - \bar{w}) (y_{i} - \bar{y})$
46.6	563	6.8	289.8	1.6	1469	108.8

表中： $w_{1} = \sqrt{x_{1}}$ ， $\bar{w} = \frac{1}{8} \sum_{i = 1}^{8} w_{i}$

(1)、根据散点图判断，

y = a + b x

与

y = c + d \sqrt{x}

，哪一个适宜作为年销售量

y

关于年宣传费

x

的回归方程类型(给出判断即可，不必说明理由)；

(2)、根据（1）的判断结果及表中数据，建立

y

关于

x

的回归方程；

(3)、根据（2）中的回归方程，求当年宣传费

x = 36

千元时，年销售预报值是多少？

附：对于一组数据 $(u_{1} ， v_{1})$ ， $(u_{2} ， v_{2})$ ，…， $(u_{n} ， v_{n})$ ，其回归线 $v = α + β u$ 的斜率和截距的最小二乘估计分别为： $\hat{β} = \frac{\sum_{i = 1}^{8} (u_{i} - \bar{u}) (v_{i} - \bar{v})}{\sum_{i = 1}^{8} {(u_{i} - \bar{u})}^{2}}$ ， $\hat{α} = \bar{v} - \hat{β} \bar{u}$ .

查看试题解析

22. 已知函数 $f (x) = \ln x + a x^{2} - (a + 2) x$ $(a \in R)$
（Ⅰ）若 $a = 0$ ，求曲线 $y = f (x)$ 在 $x = 1$ 处的切线方程；

（Ⅱ）若 $f (x)$ 存在极小值点 $t$ ，证明 $f (t) \leq - 2$ ．

查看试题解析