山东省淄博市周村区2020-2021学年九年级上学期期末数学试题

试卷更新日期：2021-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 已知：在Rt△ABC中，∠C=90°，sinA= $\frac{3}{4}$ ，则cosB的值为（）

A、 $\frac{\sqrt{7}}{4}$ B、 $\frac{4}{5}$ C、 $\frac{3}{5}$ D、 $\frac{3}{4}$

查看试题解析
2. 如图， $A$ 是反比例函数 $y = \frac{k}{x} (k \neq 0)$ 图象上第二象限内的一点， $A B ⊥ x$ 轴，垂足为 $B$ ，若 $Δ A B O$ 的面积为2，则 $k$ 的值为（）

A、-4 B、-2 C、2 D、4

查看试题解析
3. 如图，拦水坝的横断面是梯形，高 $B C = 6$ 米，斜面坡度为 $1 ： 2$ ，则斜坡 $A B$ 的长为（）

A、 $4 \sqrt{3}$ 米 B、 $6 \sqrt{5}$ 米 C、 $12 \sqrt{5}$ 米 D、 $12$ 米

查看试题解析
4. 如图所示的立体图形，其俯视图正确的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，线段 $A B$ 是 $⊙ O$ 的直径， $C ， D$ 为 $⊙ O$ 上两点，如果 $A B = 4 ， A C = 2$ ，那么 $∠ A D C$ 的度数是（）

A、15° B、30° C、45° D、60°

查看试题解析
6. 已知圆锥的母线长为5cm ，高为4cm ，则该圆锥侧面展开图的圆心角是（）

A、216° B、270° C、288° D、300°

查看试题解析
7. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则下列关于该函数说法中正确的是（）

A、 $b < 0$ B、 $c > 0$ C、 $a + b + c = 0$ D、 $b^{2} - 4 a c < 0$

查看试题解析
8. 如图，点 $I$ 和 $O$ 分别是 $Δ A B C$ 的内心和外心，若 $∠ A I B = 125 °$ ，则 $∠ A O B =$ （）

A、 $120 °$ B、 $125 °$ C、 $135 °$ D、 $140 °$

查看试题解析
9. 经过一T字型路口的行人，可能右拐，可能左拐．假设这两种可能性相同．有3人经过该路口，至少一人左拐的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{3}{8}$ C、 $\frac{3}{4}$ D、 $\frac{7}{8}$

查看试题解析
10. 如图1，点P从△ABC的顶点A出发，沿A﹣B﹣C匀速运动，到点C停止运动.点P运动时，线段AP的长度y与运动时间x的函数关系如图2所示，其中D为曲线部分的最低点，则△ABC的面积是（）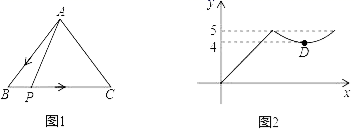

A、10 B、12 C、20 D、24

查看试题解析
11. 如图是由边长相同的小正方形组成的网格， $A$ ， $B$ ， $P$ ， $Q$ 四点均在正方形网格的格点上，线段 $A B$ ， $P Q$ 相交于点 $M$ ，则图中 $\cos ∠ Q M B$ 的值是（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{10}}{5}$

查看试题解析
12. 如图，在圆 $O$ 中，半径 $O A = \sqrt{61}$ ，弦 $B C = 10$ ，点 $Q$ 是劣弧 $A C$ 上的一个动点，连接 $B Q$ ，作 $C P ⊥ B Q$ ，垂足为 $P$ ．在点 $Q$ 移动的过程中，线段 $A P$ 的最小值是（）

A、6 B、7 C、8 D、9

查看试题解析

二、填空题

13. 若2cosα=1，则锐角α=度．

查看试题解析
14. 若点 $A (4 ， 3)$ ， $B (2 ， m)$ 在同一个反比例函数的图象上，则 $m$ 的值为．

查看试题解析
15. 如图，在正方形网格中， $A$ ， $B$ ， $C$ ， $D$ ， $E$ 都是格点，则 $∠ B A C + ∠ C D E =$ ．

查看试题解析
16. 如图，点 $P$ 是正方形 $A B C D$ 外接圆的劣弧 $A D$ 上的一点，则代数式 $\frac{P A + P C}{P B}$ 的值是．

查看试题解析

三、解答题

17. 如图，在 $⊙ O$ 中， $A C // O B$ ， $O C = 4$ ， $A B = 5$ ，则 $B C =$ ．

查看试题解析
18. 如图，在△ABC中，∠C=90°，AB的垂直平分线分别交边AB、BC于点D、E，连结AE．

(1)、如果∠B=25°，求∠CAE的度数；

(2)、如果CE=2， $\sin ∠ C A E = \frac{2}{3}$ ，求 $\tan B$ 的值．

查看试题解析
19. 一个不透明的布袋中有完全相同的三个小球，把它们分别标号为1，2，3. 小林和小华做一个游戏，按照以下方式抽取小球：先从布袋中随机抽取一个小球，记下标号后放回布袋中搅匀，再从布袋中随机抽取一个小球，记下标号. 若两次抽取的小球标号之和为奇数，小林赢；若标号之和为偶数，则小华赢.

(1)、用画树状图或列表的方法，列出前后两次取出小球上所标数字的所有可能情况；

(2)、请判断这个游戏是否公平，并说明理由.

查看试题解析
20. 已知一个二次函数图象上部分点的横坐标 $x$ 与纵坐标 $y$ 的对应值如下表所示：

$x$

$\dots$

-1

0

1

2

3

$\dots$

$y$

$\dots$

0

3

4

3

0

$\dots$

(1)、求这个二次函数的表达式；

(2)、在给定的平面直角坐标系中画出这个二次函数的图象；

(3)、结合图象，直接写出当 $y < 0$ 时， $x$ 的取值范围．

查看试题解析
21. 如图，在平面直角坐标系 $x O y$ 中，直线 $y = 2 x$ 与函数 $y = \frac{m}{x} (x > 0)$ 的图象交于点 $A (1 ， 2)$ ．

(1)、求 $m$ 的值；

(2)、过点 $A$ 作 $x$ 轴的平行线 $l$ ，直线 $y = 2 x + b$ 与直线 $l$ 交于点 $B$ ，与函数 $y = \frac{m}{x} (x > 0)$ 的图象交于点 $C$ ，与 $x$ 轴交于点 $D$ ．
①当点 $C$ 是线段 $B D$ 的中点时，求 $b$ 的值；

②当 $B C > B D$ 时，直接写出 $b$ 的取值范围．

查看试题解析
22. 如图，AB是⊙O的直径，BC交⊙O于点D，E是 $\overset{⌢}{B D}$ 的中点，连接AE交BC于点F，∠ACB=2∠EAB．

(1)、求证：AC是⊙O的切线；

(2)、若cosC= $\frac{2}{3}$ ，AC=6，求BF的长．

查看试题解析
23. 如图， $A B$ 是半圆 $O$ 的直径， $C$ 是 $\overset{⌢}{A B}$ 的中点，点 $D$ 在 $\overset{⌢}{A C}$ 上， $A C$ ， $B D$ 相交于点 $E$ ，点 $F$ 是 $B D$ 上的一点，且 $B F = A D$ ．

(1)、求证： $C F ⊥ C D$ ；

(2)、连接 $A F$ ，若 $∠ C A F = 2 ∠ A B F$ ．
①求证： $A C = A F$ ；

②当 $Δ A C F$ 的面积为 $12$ 时，求 $A C$ 的长．

查看试题解析
24. 如图，抛物线 $y = - x^{2} + bx + c$ 与直线 $y = \frac{1}{2} x + 2$ 交于C，D两点，其中点C在y轴上，点D的坐标为 $(3 ， \frac{7}{2})$ .点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点F.

(1)、求抛物线的解析式；

(2)、若点P的横坐标为m，当m为何值时，以O，C，P，F为顶点的四边形是平行四边形？请说明理由；

(3)、若存在点P，使∠PCF=45⁰ ，请直接写出相应的点P的坐标.

查看试题解析

$x$	$\dots$	-1	0	1	2	3	$\dots$
$y$	$\dots$	0	3	4	3	0	$\dots$